解:(1)存在.
∵x
1,x
2是一元二次方程(m-3)x
2+2mx+m=0的兩個實數根,
∴m-3≠0且△=4m
2-4(m-3)•m≥0,
∴m的取值范圍為m≥0且m≠3,
根據根與系數的關系得x
1+x
2=-

,x
1•x
2=

,
∵-x
1+x
1x
2=4+x
2,
∴x
1x
2=4+x
1+x
2,
∴

=4-

,
∴m=12;
(2)∵|x
1-x
2|=

,
∴(x
1-x
2)
2=3,即(x
1+x
2)
2-4x
1x
2=3,
∴(-

)
2-4×

=3,解得m
1=1,m
2=9,
當m=1時,原方程變形為2x
2-2x-1=0,解得x
1=

,x
2=
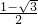
;
當m=9時,原方程變形為2x
2+6x+3=0,解得x
1=

,x
2=
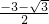
.
分析:(1)先根據根的判別式得到m的取值范圍為m≥0且m≠3,再根據根與系數的關系得x
1+x
2=-

,x
1•x
2=

,然后利用-x
1+x
1x
2=4+x
2得

=4-

,再解關于m的方程即可;
(2)先利用完全平方公式變形得到(x
1-x
2)
2=3,即(x
1+x
2)
2-4x
1x
2=3,再把x
1+x
2=-

,x
1•x
2=

代入得到(-

)
2-4×

=3,解得m
1=1,m
2=9,
然后分別把m的值代入原方程,并且利用公式法解方程.
點評:本題考查了一元二次方程ax
2+bx+c=0(a≠0)的根與系數的關系:若方程兩個為x
1,x
2,則x
1+x
2=-

,x
1•x
2=

.也考查了一元二次方程根的判別式.

 ,x1•x2=
,x1•x2= ,把它們稱為一元二次方程根與系數關系定理,請利用此定理解答一下問題:
,把它們稱為一元二次方程根與系數關系定理,請利用此定理解答一下問題: ,求m的值和此時方程的兩根.
,求m的值和此時方程的兩根. ,x1•x2=
,x1•x2= ,
, =4-
=4- ,
, ,
, )2-4×
)2-4× =3,解得m1=1,m2=9,
=3,解得m1=1,m2=9, ,x2=
,x2=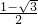 ;
; ,x2=
,x2=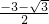 .
. ,x1•x2=
,x1•x2= ,然后利用-x1+x1x2=4+x2得
,然后利用-x1+x1x2=4+x2得 =4-
=4- ,再解關于m的方程即可;
,再解關于m的方程即可; ,x1•x2=
,x1•x2= 代入得到(-
代入得到(- )2-4×
)2-4× =3,解得m1=1,m2=9,
=3,解得m1=1,m2=9, ,x1•x2=
,x1•x2= .也考查了一元二次方程根的判別式.
.也考查了一元二次方程根的判別式. 
