
【題目】某校在校園藝術節期間舉行學生書畫大賽活動,準備購買甲、乙兩種文具,獎勵在活動中表現優秀的學生.已知購買2個甲種文具、1個乙種文具共需花費35元;購買1個甲種文具、3個乙種文具共需花費30元.
(1)求購買一個甲種文具、一個乙種文具各需多少元?
(2)若學校計劃購買這兩種文具共120個,投入資金不少于95元又不多于1000元,問有多少種購買方案?
 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中數學 來源: 題型:
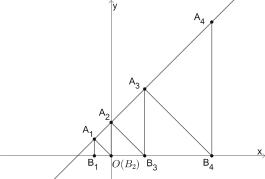
【題目】在平面直角坐標系中,點![]() 在直線
在直線![]() 上,過點
上,過點![]() 作
作![]() 軸于點
軸于點![]() ,作等腰直角三角形
,作等腰直角三角形![]() (
(![]() 與原點
與原點![]() 重合),再以
重合),再以![]() 為腰作等腰直角三角形
為腰作等腰直角三角形![]() ,以
,以![]() 為腰作等腰直角三角形
為腰作等腰直角三角形![]() ,…按照這樣的規律進行下去,那么
,…按照這樣的規律進行下去,那么![]() 的坐標為( )
的坐標為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某海域有A、B、C三艘船正在捕魚作業,C船突然出現故障,向A、B兩船發出緊急求救信號,此時B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏東33°方向,同時又位于B船的北偏東78°方向.
(1)求∠ABC的度數;
(2)A船以每小時30海里的速度前去救援,問多長時間能到出事地點.(結果精確到0.01小時).
(參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在菱形ABCD中,∠ABC=60°,P、Q是對角線BD上的兩個動點,點P從點D出發沿BD方向以1cm/s的速度向點B運動,運動終點為B;點Q從點B出發沿著BD的方向以2cm/s的速度向點D運動,運動終點為D.兩點同時出發,設運動時間為x(s),以A、Q、C、P為頂點的圖形面積為y(cm2),y與x的函數圖像如圖②所示,根據圖像回答下列問題:
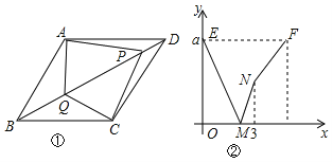
(1)BD= ,a= ;
(2)當x為何值時,以A、Q、C、P為頂點的圖形面積為4![]() cm2?
cm2?
(3)在整個運動的過程中,若△AQP為直角三角形,請直接寫出符合條件的所有x的值:.
查看答案和解析>>
科目:初中數學 來源: 題型:
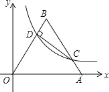
【題目】如圖,將邊長為10的正三角形OAB放置于平面直角坐標系xOy中,C是AB邊上的動點(不與端點A,B重合),作CD⊥OB于點D,若點C,D都在雙曲線y=![]() 上(k>0,x>0),則k的值為( )
上(k>0,x>0),則k的值為( )
A. 25![]() B. 18
B. 18![]() C. 9D. 9
C. 9D. 9![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,PQ、PB、QC是⊙O的切線,切點分別為A、B、C,點D在![]() 上,若∠D=100°,則∠P與∠Q的度數之和是( )
上,若∠D=100°,則∠P與∠Q的度數之和是( )
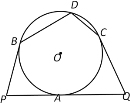
A.160°B.140°C.120°D.100°
查看答案和解析>>
科目:初中數學 來源: 題型:
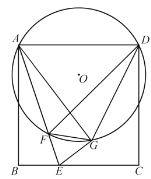
【題目】在正方形ABCD中,點E是BC邊上一動點,連接AE,沿AE將△ABE翻折得△AGE,連接DG,作△AGD的外接⊙O,⊙O交AE于點F,連接FG、FD.
(1)求證∠AGD=∠EFG;
(2)求證△ADF∽△EGF;
(3)若AB=3,BE=1,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
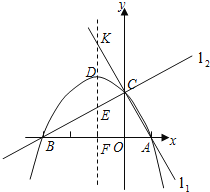
【題目】已知兩直線l1,l2分別經過點A(1,0),點B(﹣3,0),并且當兩直線同時相交于y正半軸的點C時,恰好有l1⊥l2,經過點A、B、C的拋物線的對稱軸與直線l2交于點K,如圖所示.
(1)求點C的坐標,并求出拋物線的函數解析式;
(2)拋物線的對稱軸被直線l1,拋物線,直線l2和x軸依次截得三條線段,問這三條線段有何數量關系?請說明理由;
(3)當直線l2繞點C旋轉時,與拋物線的另一個交點為M,請找出使△MCK為等腰三角形的點M,簡述理由,并寫出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
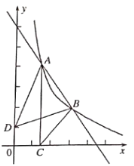
【題目】如圖,點![]() 、
、![]() 是直線
是直線![]() 與反比例函數
與反比例函數![]() 圖象的兩個交點,
圖象的兩個交點,![]() 軸于點C,己知點D(0,1),連接AD、BD、BC,
軸于點C,己知點D(0,1),連接AD、BD、BC,
(1)求反比例函數和直線AB的表達式;
(2)根據函數圖象直接寫出當![]() 時不等式
時不等式![]() 的解集;
的解集;
(3)設△ABC和△ABD的面積分別為![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com