
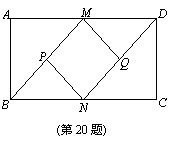
如圖,在矩形ABCD中,M、N分別AD、BC的中點,P、Q分別BM、DN
的中點.
(1)求證:四邊形MPNQ是菱形;
(2)若AB=2,BC=4,求四邊形MPNQ的面積.
 |
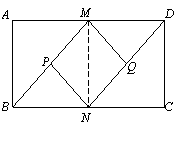
(1)證明:∵四邊形ABCD是矩形,
∴AD=BC,AD∥BC.
連結MN,∵M、N分別AD、BC的中點,
 ∴MD=
∴MD=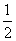 AD,BN=
AD,BN=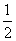 BC.
BC.
∴MD=BN,MD∥ BN,∴四邊形BNDM是平行四邊形.
BN,∴四邊形BNDM是平行四邊形.
∴MB=ND.
∵P、Q分別BM、DN的中點,∴MP=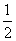 MB,NQ=
MB,NQ=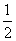 DN.
DN.
∴MP=NQ.
又∵MP∥NQ,∴四邊形MPNQ是平 行四邊形.
行四邊形.
 ∵ABCD為矩形,M、N分別AD、BC的中點,
∵ABCD為矩形,M、N分別AD、BC的中點,
∴四邊形ABNM為矩形,∴MN⊥BC.
∴在Rt△MNB中,PN=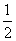 BM.∴PN=PM.
BM.∴PN=PM.
∴四邊形MPNQ是菱形.
(2)∵AB=2,BC=4,∴MN=BN=2
∵P為MB的中點,∴PN⊥MB,PN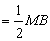
在Rt△MNB中,MB=
∴ ,∴四邊形MPNQ是邊長為
,∴四邊形MPNQ是邊長為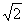 的正方形.
的正方形.
∴四邊形MPNQ的面積為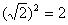


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
某批發商以40元/千克的成本價購入了某產品700千克,據市場預測,該產品的
銷售價y(元/千克)與保存時間x(天)的函數關系為y=50+2x,但保存這批產品平均每天
將損耗15千克,且最多保存15天.另外,批發商每天保存該批產品的費用為50元.
(1)若批發商在保存該產品5天時一次性賣出,則可獲利 元.
(2)如果批發商希望通過這批產品賣出獲利10000元,則批發商應在保存該產品多少
天時一次性賣出?
查看答案和解析>>
科目:初中數學 來源: 題型:
反比例函數y= 和正比例函數y=mx的部分圖象如圖所示.
和正比例函數y=mx的部分圖象如圖所示.
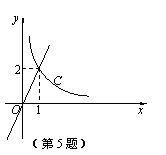 由此可以得到方程
由此可以得到方程 =mx的實數根為
=mx的實數根為
| A.x=1 | B.x=2 |
| C.x1=1,x2=-1 | D.x1=1,x2=-2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
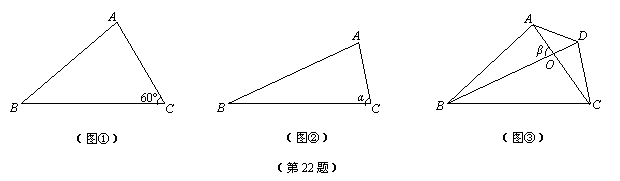
(1)如圖①,若BC=6,AC=4,∠C=60°,求△ABC的面積S△ABC ;
(2)如圖②,若BC=a,AC=b,∠C=α,求△ABC的面積S△ABC ;
(3)如圖③,四邊形ABCD,若AC=m,BD=n,對角線AC、BD交于O點,它們所成
的銳角為β.求四邊形ABCD的面積S四邊形ABCD .
查看答案和解析>>
科目:初中數學 來源: 題型:
某啤酒廠搞捉銷活動,一箱24瓶啤酒中有4瓶的瓶蓋內印有“獎”字.小明的爸爸買了
一箱這種品牌的啤酒,他連續打開了其中的4瓶均未中獎. 這時小明在剩下的啤酒中任
這時小明在剩下的啤酒中任
意打開一瓶,中獎的可能性是 ( ).
A. 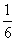 B.
B. C.
C. 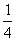 D.
D. 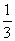
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com