
【題目】已知函數(shù) ![]() 是關于x的二次函數(shù),求:
是關于x的二次函數(shù),求:
(1)滿足條件的m的值;
(2)m為何值時,拋物線有最低點?求出這個最低點,當x為何值時,y隨x的增大而增大;
(3)m為何值時,拋物線有最大值?最大值是多少?當x為何值時,y隨x的增大而減小?
【答案】
(1)
解:由題意,有 ![]() 且
且 ![]() ,解之得
,解之得 ![]() 或
或 ![]() .
.
(2)
解:當 ![]() 時,二次函數(shù)有最低點,此時
時,二次函數(shù)有最低點,此時 ![]() ,最低點為(0,0),且當
,最低點為(0,0),且當 ![]() 時,y隨x的增大而增大.
時,y隨x的增大而增大.
(3)
解:當 ![]() 時,拋物線有最大值,最大值為0,且當
時,拋物線有最大值,最大值為0,且當 ![]() 時,y隨x的增大而減小.
時,y隨x的增大而減小.
【解析】二次函數(shù) ![]() 當
當 ![]() 取正負值時,拋物線開口方向改變,增減性改變。
取正負值時,拋物線開口方向改變,增減性改變。
【考點精析】解答此題的關鍵在于理解二次函數(shù)圖象以及系數(shù)a、b、c的關系的相關知識,掌握二次函數(shù)y=ax2+bx+c中,a、b、c的含義:a表示開口方向:a>0時,拋物線開口向上; a<0時,拋物線開口向下b與對稱軸有關:對稱軸為x=-b/2a;c表示拋物線與y軸的交點坐標:(0,c).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,函數(shù)y=![]() 和y= - x+4的圖像交點為A、B,原點為O,求△AOB面積.
和y= - x+4的圖像交點為A、B,原點為O,求△AOB面積.

【答案】8![]()
【解析】整體分析:
聯(lián)立方程y=![]() 和y= - x+4,求出點A,B的坐標,然后由公式△OAB的面積=
和y= - x+4,求出點A,B的坐標,然后由公式△OAB的面積=![]() ×(x1- x2)(y2- y1)求解.
×(x1- x2)(y2- y1)求解.
解:把y=![]() 代入y= - x+4得,
代入y= - x+4得,
![]() = - x+4,
= - x+4,
解得x1=2+![]() ,x2=2-
,x2=2-![]() .
.
所以y1=2-![]() ,y2=2+
,y2=2+![]() .
.
則A(2-![]() ,2+
,2+![]() ),B(2+
),B(2+![]() ,2-
,2-![]() ),
),
所以△OAB的面積=![]() ×(x1- x2)(y2- y1)==
×(x1- x2)(y2- y1)==![]() ×4
×4![]() ×4
×4![]() =
=![]() .
.
【題型】解答題
【結束】
19
【題目】如圖,直線![]() 與雙曲線
與雙曲線![]() 相交于A(2,1)、B兩點.
相交于A(2,1)、B兩點.

(1)求m及k的值;
(2)不解關于x、y的方程組 直接寫出點B的坐標;
直接寫出點B的坐標;
(3)直線![]() 經(jīng)過點B嗎?請說明理由.
經(jīng)過點B嗎?請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1在正方形ABCD中,P是對角線BD上的一點,點E在AD的延長線上,且PA=PE,PE交CD于F.
(1)證明:PC=PE;
(2)求∠CPE的度數(shù);
(3)如圖2,把正方形ABCD改為菱形ABCD,其他條件不變,當∠ABC=120度時,連接CE,試探究線段AP與線段CE的數(shù)量關系,并說明理由.
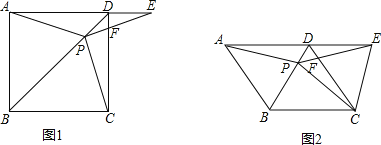
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列說法錯誤的是( )
A.在二次函數(shù) ![]() 中,當
中,當 ![]() 時,
時, ![]() 隨
隨 ![]() 的增大而增大
的增大而增大
B.在二次函數(shù) ![]() 中,當
中,當 ![]() 時,
時, ![]() 有最大值
有最大值 ![]()
C.![]() 越大圖象開口越小,
越大圖象開口越小, ![]() 越小圖象開口越大
越小圖象開口越大
D.無論 ![]() 是正數(shù)或負數(shù),
是正數(shù)或負數(shù), ![]()
![]() 的頂點一定是坐標原點
的頂點一定是坐標原點
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列說法正確的是( ).
A. m=-2是方程m-2=0的解 B. m=6是方程3m+18=0的解
C. x=-1是方程-![]() =0的解 D. x=
=0的解 D. x=![]() 是方程10x=1的解
是方程10x=1的解
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,在ABCD中,點E,F(xiàn)在對角線BD上,且BE=DF,
求證:(1)AE=CF;(2)四邊形AECF是平行四邊形.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知一次函數(shù)y=mx﹣3m2+12,請按要求解答問題:
(1)m為何值時,函數(shù)圖象過原點,且y隨x的增大而減小?
(2)若函數(shù)圖象平行于直線y=﹣x,求一次函數(shù)解析式;
(3)若點(0,﹣15)在函數(shù)圖象上,求m的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為了了解某市九年級學生學業(yè)考試體育成績,現(xiàn)從中隨機抽取部分學生的體育成績進行分段(A:50分; B:49-45分;C:44-40分;D:39-30分;E:29-0分).每段包含最高分,不包含最低分,統(tǒng)計表如下,統(tǒng)計圖如圖所示.
分數(shù)段 | 頻數(shù)(人) | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

根據(jù)上面提供的信息,回答下列問題:
(1)在統(tǒng)計表中,![]() 的值為___,
的值為___, ![]() 的值為__,并將統(tǒng)計圖補充完整.
的值為__,并將統(tǒng)計圖補充完整.
(2)成績在40分以上定為優(yōu)秀,那么該市今年10440名九年級學生中體育成績?yōu)閮?yōu)秀的學生約有多少名?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某農(nóng)場擬建三件矩形飼養(yǎng)室,飼養(yǎng)室一面靠現(xiàn)有墻(墻可用長≤20m),中間用兩道墻隔開,已知計劃中的建筑材料可建圍墻的總長為60m,設飼養(yǎng)室寬為x(m),總占地面積為y(m2)(如圖所示). 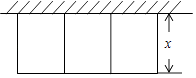
(1)求y關于x的函數(shù)表達式,并直接寫出自變量x的取值范圍;
(2)三間飼養(yǎng)室占地總面積有可能達到210m2嗎?請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com