
【題目】已知:如圖,在平面直角坐標系中,一次函數y=ax+b(a≠0)的圖象與反比例函數![]() 的圖象交于一、三象限內的A、B兩點,與x軸交于C點,點A的坐標為(2,m),點B的坐標為(n,﹣2),tan∠BOC=
的圖象交于一、三象限內的A、B兩點,與x軸交于C點,點A的坐標為(2,m),點B的坐標為(n,﹣2),tan∠BOC=![]() .
.
(1)求該反比例函數和一次函數的解析式;
(2)在x軸上有一點E(O點除外),使得△BCE與△BCO的面積相等,求出點E的坐標.
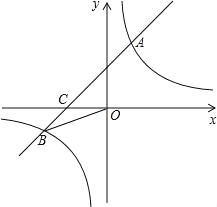
【答案】(1)一次函數解析式為y=x+3;
(2)E(﹣6,0)
【解析】
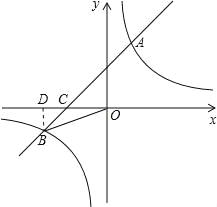
試題分析:(1)過B點作BD⊥x軸,垂足為D,由B(n,﹣2)得BD=2,由tan∠BOC=![]() ,解直角三角形求OD,確定B點坐標,得出反比例函數關系式,再由A、B兩點橫坐標與縱坐標的積相等求n的值,由“兩點法”求直線AB的解析式;
,解直角三角形求OD,確定B點坐標,得出反比例函數關系式,再由A、B兩點橫坐標與縱坐標的積相等求n的值,由“兩點法”求直線AB的解析式;
(2)點E為x軸上的點,要使得△BCE與△BCO的面積相等,只需要CE=CO即可,根據直線AB解析式求CO,再確定E點坐標.
試題解析:(1)過B點作BD⊥x軸,垂足為D,
∵B(n,﹣2),
∴BD=2,
在Rt△OBD中,tan∠BOC=![]() ,即
,即![]() =
=![]() ,
,
解得OD=5,
又∵B點在第三象限,
∴B(﹣5,﹣2),
將B(﹣5,﹣2)代入y=![]() 中,得k=xy=10,
中,得k=xy=10,
∴反比例函數解析式為y=![]() ,
,
將A(2,m)代入y=![]() 中,得m=5,
中,得m=5,
∴A(2,5),
將A(2,5),B(﹣5,﹣2)代入y=ax+b中,
得![]() ,
,
解得![]() .
.
則一次函數解析式為y=x+3;
(2)由y=x+3得C(﹣3,0),即OC=3,
∵S△BCE=S△BCO,
∴CE=OC=3,
∴OE=6,即E(﹣6,0).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】小明去超市買三種商品.其中丙商品單價最高.如果購買3件甲商品、2件乙商品和1件丙商品,那么需要付費20元,如果購買4件甲商品,3件乙商品和2件丙商品,那么需要付費32元.
(1)如果購買三種商品各1件,那么需要付費多少元?
(2)如果需要購買1件甲商品,3件乙商品和2件丙商品,那么小明至少需多少錢才能保證一定能全部買到?(結果精確到元)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校計劃用104 000元購置一批電腦(這批款項須恰好用完,不得剩余或追加).經過招標,其中平板電腦每臺1600元,臺式電腦每臺4000元,筆記本電腦每臺4600元.
(1)若學校同時購進其中兩種不同類型的電腦共50臺,請你幫學校設計該如何購買;
(2)若學校同時購進三種不同類型的電腦共26臺(三種類型的電腦都有),并且要求筆記本電腦的購買量不少于15臺.
查看答案和解析>>
科目:初中數學 來源: 題型:
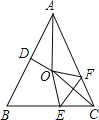
【題目】如圖,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的角平分線與AB的中垂線交于點O,點C沿EF折疊后與點O重合,則∠CEF的度數是______________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com