
【題目】如圖,拋物線y=﹣ ![]() x2+bx+e與x軸交于點A(﹣3,0)、點B(9,0),與y軸交于點C,頂點為D,連接AD、DB,點P為線段AD上一動點.
x2+bx+e與x軸交于點A(﹣3,0)、點B(9,0),與y軸交于點C,頂點為D,連接AD、DB,點P為線段AD上一動點.
(1)求拋物線的解析式;
(2)如圖1,過點P作BD的平行線,交AB于點Q,連接DQ,設AQ=m,△PDQ的面積為S,求S關于m的函數解析式,以及S的最大值;
(3)如圖2,拋物線對稱軸與x軸交與點G,E為OG的中點,F為點C關于DG對稱的對稱點,過點P分別作直線EF、DG的垂線,垂足為M、N,連接MN,直接寫出△PMN為等腰三角形時點P的坐標.
【答案】
(1)
解:∵a=﹣ ![]() ,拋物線與x軸交與點A(﹣3,0),點B(9,0),
,拋物線與x軸交與點A(﹣3,0),點B(9,0),
∴可以假設拋物線解析式為y=﹣ ![]() (x+3)(x﹣9)=﹣
(x+3)(x﹣9)=﹣ ![]() x2+
x2+ ![]() x+6,
x+6,
∴拋物線解析式為y=﹣ ![]() x2+
x2+ ![]() x+6,
x+6,
(2)
解:∵y=﹣ ![]() x2+
x2+ ![]() x+6=﹣
x+6=﹣ ![]() (x﹣3)2+8,
(x﹣3)2+8,
∴頂點D坐標(3,8),
∵AD=DB=10,
∴∠DAB=∠DBA,
∵PQ∥BD,
∴∠PQA=∠DBA,
∴∠PAQ=∠PQA,
∴PA=PQ,
∴△PAQ為等腰三角形,
作PH⊥AQ于H,則AH=HQ= ![]() (如圖1中),
(如圖1中),
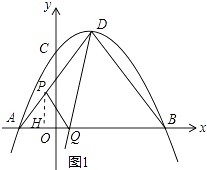
∴tan∠DAB= ![]() =
= ![]() ,
,
∴PH= ![]() m,
m,
∴S=S△ADQ﹣S△APQ= ![]() m8﹣
m8﹣ ![]() m
m ![]() m=﹣
m=﹣ ![]() m2+4m=﹣
m2+4m=﹣ ![]() (m﹣6)2+12,
(m﹣6)2+12,
∴當m=6時,S最大值=12.
(3)
解:∵E( ![]() ,0),F(6,6),
,0),F(6,6),
∴直線EF解析式為y= ![]() x﹣2,直線AD解析式為y=
x﹣2,直線AD解析式為y= ![]() x+4,
x+4,
∴EF∥AD,作EL⊥AD于L,(如圖2中)
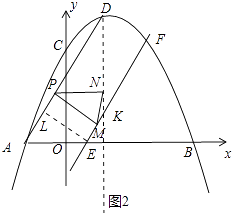
∵AE= ![]() ,sin∠DAB=
,sin∠DAB= ![]() ,
,
∴LE= ![]() ×
× ![]() =
= ![]() =PM,
=PM,
①PM=PN= ![]() 時,
時,
∴xP=3﹣ ![]() =﹣
=﹣ ![]() ,yP=﹣
,yP=﹣ ![]() ×
× ![]() +4=
+4= ![]() ,
,
∴P(﹣ ![]() ,
, ![]() ),
),
∴直線PM解析式為y=﹣ ![]() x+
x+ ![]() ,
,
由 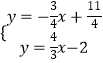 ,解得
,解得 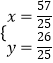 ,
,
∴點M( ![]() ,
, ![]() )
)
∴EM= ![]() =
= ![]() .
.
②NP=NM時,設直線EF與對稱軸交于點K,K(3,2),
此時點N在PM的垂直平分線上,DN=NK,
∴N(3,5),P( ![]() ,5),
,5),
∴直線PM的解析式為y=﹣ ![]() x+
x+ ![]() ,
,
由 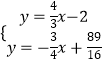 ,解得
,解得 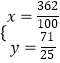 ,
,
∴M( ![]() ,
, ![]() ),
),
∴EM= ![]() =
= ![]() ,
,
③PM=MN時,cos∠MPN= ![]() =
= ![]() ,
,
∴PN= ![]() ,由此可得P(﹣
,由此可得P(﹣ ![]() ,
, ![]() ),
),
∴直線PM解析式為y=﹣ ![]() x﹣
x﹣ ![]() ,
,
由 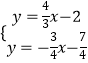 解得
解得 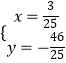 ,
,
∴M( ![]() ,﹣
,﹣ ![]() ),
),
∴EM= ![]() =
= ![]() .
.
綜上所述,EM= ![]() 或
或 ![]() 或
或 ![]() .
.
【解析】(1)可以假設拋物線解析式為y=﹣ ![]() (x+3)(x﹣9),展開化簡即可.(2)作PH⊥AQ于H,則AH=HQ=
(x+3)(x﹣9),展開化簡即可.(2)作PH⊥AQ于H,則AH=HQ= ![]() (如圖1中),根據S=S△ADQ﹣S△APQ構建二次函數,利用二次函數的性質即可解決問題.(3)分三種情形討論①PM=PN,②NP=NM,③MN=MP,分別求出直線PM的解析式,利用方程組求出點M坐標即可解決問題.
(如圖1中),根據S=S△ADQ﹣S△APQ構建二次函數,利用二次函數的性質即可解決問題.(3)分三種情形討論①PM=PN,②NP=NM,③MN=MP,分別求出直線PM的解析式,利用方程組求出點M坐標即可解決問題.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,若干個半徑為2個單位長度,圓心角為60°的扇形組成一條連續的曲線,點P從原點O出發,沿這條曲線向右上下起伏運動,點在直線上的速度為2個單位長度/秒,點在弧線上的速度為 ![]() 個單位長度/秒,則2017秒時,點P的坐標是( )
個單位長度/秒,則2017秒時,點P的坐標是( ) 
A.(2017,0)
B.(2017, ![]() )
)
C.(2017,﹣ ![]() )
)
D.(2016,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綠色無公害蔬菜基地有甲、乙兩種植戶,他們種植了A,B兩類蔬菜,兩種植戶種植的兩類蔬菜的種植面積與總收入如下表:
種植戶 | 種植A類蔬菜面積 | 種植B類蔬菜面積 | 總收入 |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
說明:不同種植戶種植的同類蔬菜每畝的平均收入相等;畝為土地面積單位.
(1)求A、B兩類蔬菜每畝的平均收入各是多少元;
(2)某種植戶準備租20畝地用來種植A、B兩類蔬菜,為了使總收入不低于63000元,且種植A類蔬菜的面積多于種植B類蔬菜的面積(兩類蔬菜的種植面積均為整數),求該種植戶所有租地方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現要把192噸物資從我市運往甲、乙兩地,用大、小兩種貨車共18輛恰好能一次性運完這批物資.已知這兩種貨車的載重量分別為14噸/輛和8噸/輛,運往甲、乙兩地的運費如表:
運往地 | 甲地(元/輛) | 乙地(元/輛) |
大貨車 | 720 | 800 |
小貨車 | 500 | 650 |
(1)求這兩種貨車各用多少輛?
(2)如果安排10輛貨車前往甲地,其余貨車前往乙地,其中前往甲地的大貨車為a輛,前往甲、乙兩地的總運費為w元,求出w與a的函數關系式;
(3)在(2)的條件下,若運往甲地的物資部少于96噸,請你設計出使總運費最低的貨車調配方案,并求出最少總運費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小華在一起玩數字游戲,他們每人取了一張數字卡片,拼成了一個兩位數. 小明說:“哇!這個兩位數的十位數字與個位數字之和恰好是9.”他們又把這兩張卡片對調,得到了一個新的兩位數,小華說:“這個兩位數恰好比原來的兩位數大9.”那么,你能回答以下問題嗎?
他們取出的兩張卡片上的數字分別是多少?
第一次,他們拼成的兩位數是多少?
第二次,他們拼成的兩位數又是多少呢?請你好好動動腦筋喲!
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=x2+bx+c與x軸交于A、B兩點(A點在B點左側),與y軸交于點C(0,﹣3),對稱軸是直線x=1,直線BC與拋物線的對稱軸交于點D.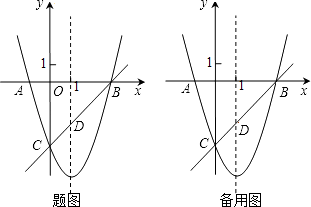
(1)求拋物線的函數表達式;
(2)求直線BC的函數表達式;
(3)點E為y軸上一動點,CE的垂直平分線交CE于點F,交拋物線于P、Q兩點,且點P在第三象限.
①當線段PQ= ![]() AB時,求tan∠CED的值;
AB時,求tan∠CED的值;
②當以點C、D、E為頂點的三角形是直角三角形時,請直接寫出點P的坐標.
溫馨提示:考生可以根據第(3)問的題意,在圖中補出圖形,以便作答.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過原點的直線y=k1x和y=k2x與反比例函數y= ![]() 的圖象分別交于兩點A,C和B,D,連接AB,BC,CD,DA.
的圖象分別交于兩點A,C和B,D,連接AB,BC,CD,DA.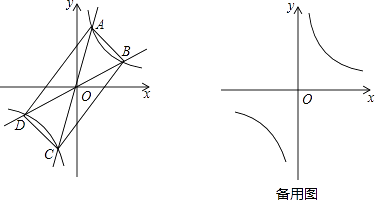
(1)四邊形ABCD一定是四邊形;(直接填寫結果)
(2)四邊形ABCD可能是矩形嗎?若可能,試求此時k1 , k2之間的關系式;若不能,說明理由;
(3)設P(x1 , y1),Q(x2 , y2)(x2>x1>0)是函數y= ![]() 圖象上的任意兩點,a=
圖象上的任意兩點,a= ![]() ,b=
,b= ![]() ,試判斷a,b的大小關系,并說明理由.
,試判斷a,b的大小關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com