
【題目】點![]() 在數軸上表示的數是
在數軸上表示的數是![]() ,且滿足
,且滿足![]() ,多項式
,多項式![]() 是五次四項式.
是五次四項式.
(1)則![]() 的值為 ,
的值為 ,![]() 的值為 ,
的值為 ,![]() 的值為 ;
的值為 ;
(2)已知點![]() 是數軸上的兩個動點,點
是數軸上的兩個動點,點![]() 從點
從點![]() 出發,以每秒3個單位的速度向右運動,同時點
出發,以每秒3個單位的速度向右運動,同時點![]() 從點
從點![]() 出發,以每秒4個單位的速度向左運動:
出發,以每秒4個單位的速度向左運動:
①若點![]() 和點
和點![]() 經過
經過![]() 秒后,在數軸上的點
秒后,在數軸上的點![]() 處相遇,求
處相遇,求![]() 的值和點
的值和點![]() 所表示的數;
所表示的數;
②若點![]() 運動到點
運動到點![]() 處,點
處,點![]() 再出發,則點
再出發,則點![]() 運動幾秒后兩點之間的距離為8個單位長度.
運動幾秒后兩點之間的距離為8個單位長度.
【答案】(1)![]() ;
;![]() ;
;![]() ;(2)①t的值為4,點D所表示的數是4;②點Q運動
;(2)①t的值為4,點D所表示的數是4;②點Q運動![]() 秒或
秒或![]() 秒后兩點之間的距離為8個單位長度
秒后兩點之間的距離為8個單位長度
【解析】
(1)利用偶次方及絕對值的非負性,可求出![]() 的值,再利用多項式的定義可求出
的值,再利用多項式的定義可求出![]() 的值;
的值;
(2)①當運動時間為t秒時,點P所表示的數是![]() ,點Q所表示的數是
,點Q所表示的數是![]() ,由點P,Q相遇,可得出關于t的一元一次方程,解之即可得出結論;
,由點P,Q相遇,可得出關于t的一元一次方程,解之即可得出結論;
②當運動時間為t秒時,點P所表示的數是![]() ,點Q所表示的數是
,點Q所表示的數是![]() ,由
,由![]() ,可得出關于t的含絕對值符號的一元一次方程,解之即可得出結論.
,可得出關于t的含絕對值符號的一元一次方程,解之即可得出結論.
(1)∵![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
∵多項式![]() 是五次四項式,
是五次四項式,
∴![]() ,
,![]() ,
,
∴![]() .
.
故答案為:![]() ;
;![]() ;
;![]() ;
;
(2)①當運動時間為t秒時,點P所表示的數是![]() ,點Q所表示的數是
,點Q所表示的數是![]() ,
,
根據題意得:![]() ,
,
解得:![]() ,
,
∴![]() .
.
答:t的值為4,點D所表示的數是4;
②當運動時間為t秒時,點P所表示的數是![]() ,點Q所表示的數是
,點Q所表示的數是![]() ,
,
根據題意得:![]() ,
,
解得:![]() .
.
答:點Q運動![]() 秒或
秒或![]() 秒后兩點之間的距離為8個單位長度.
秒后兩點之間的距離為8個單位長度.


科目:初中數學 來源: 題型:
【題目】冬至過后,晝夜溫差逐漸加大,山城的市民們已然感受到了深冬的寒意.在還未普遍使用地暖供暖設備的山城,小型電取暖器仍然深受市民的青睞.某格力專賣店銷售壁掛式電暖器和鹵素/石英式取暖器(俗稱 “小太陽”),其中壁掛式電暖器的售價是“小太陽”售價的5倍還多100元,2016年12月份壁掛式電暖器和“小太陽”共銷售500臺,壁掛式電暖器與“小太陽”銷量之比是4∶1,銷售總收入為58.6萬元.
(1)分別求出每臺壁掛式電暖器和“小太陽”的售價;
(2)隨著“元旦、春節”雙節的來臨和氣溫的回升,銷售進入淡季,2017年1月份,壁掛式電暖器的售價比2016年12月下調了4m﹪,根據經驗銷售量將比2016年12月下滑6m﹪,而“小太陽”的銷售量和售價都維持不變,預計銷售總收入將下降到16.04萬元,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】三角形ABC與三角形![]() 在平面直角坐標系中的位置如圖所示,三角形
在平面直角坐標系中的位置如圖所示,三角形![]() 是由三角形ABC經過平移得到的.
是由三角形ABC經過平移得到的.
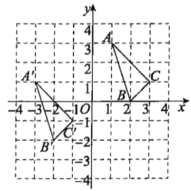
(1)分別寫出點![]()
![]()
![]() 的坐標;
的坐標;
(2)說明三角形![]() 是由三角形ABC經過怎樣的平移得到的;
是由三角形ABC經過怎樣的平移得到的;
(3)若點![]() 是三角形ABC內的一點,則平移后點P在三角形
是三角形ABC內的一點,則平移后點P在三角形![]() 內的對應點為P‘,寫出點P’的坐標.
內的對應點為P‘,寫出點P’的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一個三角形紙片的兩邊長是5和6,第三邊的長是方程x2﹣6x+5=0的一個根,若用此三角形紙片剪出一個圓,則剪出的圓的半徑最大是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,AC平分∠BAD,CE⊥AB于E,CD⊥AD于F,且BC=DC.
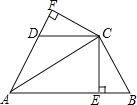
(1)BE與DF是否相等?請說明理由;
(2)若DF=1,AD=3,求AB的長;
(3)若△ABC的面積是23,△ADC面積是18,直接寫出△BEC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學習了數軸后,小亮決定對數軸進行變化應用:
(1)應用一:已知點![]() 在數軸上表示為-2,數軸上任意一點
在數軸上表示為-2,數軸上任意一點![]() 表示的數為
表示的數為![]() ,則
,則![]() 兩點的距離可以表示為 ;應用這個知識,請寫出當
兩點的距離可以表示為 ;應用這個知識,請寫出當![]() 時,
時,![]() 有最小值為 .
有最小值為 .
(2)應用二:從數軸上取下一個單位長度的線段,第一次剪掉原長的![]() ,第二次剪掉剩下的
,第二次剪掉剩下的![]() ,依此類推,每次都剪掉剩下的
,依此類推,每次都剪掉剩下的![]() ,則剪掉4次后剩下線段長度為 ;應用這個原理,請計算:
,則剪掉4次后剩下線段長度為 ;應用這個原理,請計算:![]() ;
;
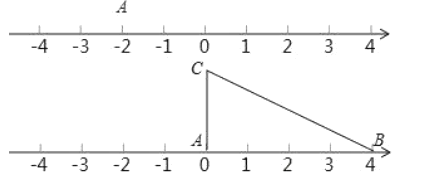
(3)應用三:如圖,將一根拉直的細線看作數軸,一個三邊長分別為![]() ,
,![]() ,
,![]() 的三角形
的三角形![]() 的頂點
的頂點![]() 與原點重合,
與原點重合,![]() 邊在數軸正半軸上,將數軸正半軸的線沿
邊在數軸正半軸上,將數軸正半軸的線沿![]() 的順序依次纏繞在三角形
的順序依次纏繞在三角形![]() 的邊上,負半軸的線沿
的邊上,負半軸的線沿![]() 的順序依次纏繞在三角形
的順序依次纏繞在三角形![]() 的邊上.
的邊上.
①如果正半軸的線纏繞了3圈,負半軸的線纏繞了5圈,求繞在點![]() 上的所有數之和;
上的所有數之和;
②如果正半軸的線不變,將負半軸的線拉長一倍,即原線上的點-2的位置對應著拉長后的數-1,并將三角形![]() 向正半軸平移一個單位后再開始繞,求繞在點
向正半軸平移一個單位后再開始繞,求繞在點![]() 且絕對值不超過60的所有數之和.
且絕對值不超過60的所有數之和.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個梯子AB長2.5米,頂端A靠在墻AC上,這時梯子下端B與墻角C距離為1.5米,梯子滑動后停在DE的位置上,測得BD長為0.5米,則梯子頂端A下落了( )米.
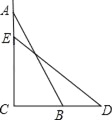
A. 0.5 B. 1 C. 1.5 D. 2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 和點
和點![]() ,交
,交![]() 軸于點
軸于點![]() .過點
.過點![]() 作
作![]() 軸,交拋物線于點
軸,交拋物線于點![]() .
.
(1)求拋物線的解析式;
(2)若直線![]() 與線段
與線段![]() 、
、![]() 分別交于
分別交于![]() 、
、![]() 兩點,過
兩點,過![]() 點作
點作![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,求矩形
,求矩形![]() 的最大面積;
的最大面積;
(3)若直線![]() 將四邊形
將四邊形![]() 分成左、右兩個部分,面積分別為
分成左、右兩個部分,面積分別為![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,∠E=∠F=90°,∠B=∠C,AE=AF,結論:①EM=FN;②AF
∥EB;③∠FAN=∠EAM;④△ACN≌△ABM![]() 其中正確的有 .
其中正確的有 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com