已知直線y=2x+4與x軸、y軸分別相交于A、C兩點,拋物線y=ax2+bx+c(a≠0)經過點A、C和x軸上的另一點B(1,0).
(1)求拋物線的解析式,并畫出函數圖象略圖;
(2)在直線AC上求點P,使以點A、B、P為頂點的三角形與△AOC相似;
(3)設拋物線的頂點為M,在拋物線上是否存在點Q,使△ABQ的面積等于△AMC面積的8倍?若存在,求出點Q的坐標;若不存在,請說明理由.
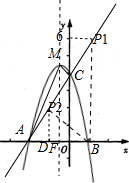
解:(1)由于直線y=2x+4與x軸、y軸相交于A、C兩點,
∴當x=0時,y=4. 當y=0時,x=-2.
∴點A的坐標為(-2,0),點C的坐標為(0,4).
又∵拋物線y=ax
2+bx+c(a≠0)
經過A(-2,O),B(1,O),C(O,4)三點,
拋物線的解析式為:y=-2x
2-2x+4.
如圖,畫出函數圖象略圖.
(2)(i)由于OC⊥AO,所以過B作BP⊥x軸,交直線AC于點P
1,
則OC∥BP
1.△ABP∽△AOC.
∵P
l點的橫坐標為1,把x=1代入y=2x+4得y=6.
∴P
1點的坐標為(1,6).
(ii)∵△AOC為直角三角形,且AO=2,OC=4,∴AC=2

.
過P
2作BP
2⊥AC交AC于P
2,在Rt△ABP
2與Rt△ACO中,∠CA0是公共角,
∴Rt△ABP
2∽Rt△ACO

=

,AP
2=

過B點作P
2D⊥X軸于D,則Rt△AP
2D∽Rt△ABP
2.
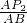
=
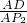
∴AD=

,OD=OA-AD=

,
∴P
2點的橫坐標為-

把X=-

代入y=2x+4得y=

.P
2點的坐標為(-

,

);
(3)存在.
拋物線y=-2x
2-2x+4頂點M的坐標為(-

,

).
假設在拋物線上存在點Q,使.S
△ABQ=8S
△AMC.
設Q的坐標為(x
Q,y
Q),對稱軸X=-

與x軸交于點F.
則S
△AMC=S
四邊形AOCM-S
△AOC=S
△AFM+S
梯形FOCM-S
△OCA=

,
S
△ABQ=

AB•|y
Q|=8×

,AB=3,|y
Q|=8,y
Q=±8.
當y
Q=8時,-2x
2-2x+4=8,即:x
2+x+2=O,
∵△=-7<O,∴此方程無解.
當y
Q=-8時,-2x
2-2x+4=-8,即:x
2+x-6=0,解之得x
1=-3,x
2=2,
∴O點的坐標為(-3,-8)或(2,-8).
∴在拋物線上存在點Q
1(-3,-8)或Q
2(2,-8),
使△ABQ的面積等于△AMC面積的8倍.
分析:(1)根據當x=0時,y=4,當y=0時,x=-2,分別求出A,B兩點坐標,再代入解析式即可求出;
(2)過B作BP⊥x軸,交直線AC于點P
1,則OC∥BP
1.△ABP∽△AOC,即可求出P點坐標,再過P
2作BP
2⊥AC交AC于P
2,在Rt△ABP
2與Rt△ACO中,求出Rt△ABP
2∽Rt△ACO 進而求出P點坐標;
(3)根據S
△AMC=S
四邊形AOCM-S
△AOC=S
△AFM+S
梯形FOCM-S
△OCA=

,以及S
△ABQ=

AB•|y
Q|=8×

,AB=3,|y
Q|=8,y
Q=±8,即可得出Q點的坐標.
點評:此題主要考查了二次函數的綜合應用以及相似三角形的判定與性質和待定系數法求二次函數解析式等知識,利用數形結合進行分析得出是解題關鍵.

 解:(1)由于直線y=2x+4與x軸、y軸相交于A、C兩點,
解:(1)由于直線y=2x+4與x軸、y軸相交于A、C兩點, .
. =
= ,AP2=
,AP2=
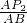 =
=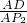
 ,OD=OA-AD=
,OD=OA-AD= ,
,
 代入y=2x+4得y=
代入y=2x+4得y= .P2點的坐標為(-
.P2點的坐標為(- ,
, );
); ,
, ).
). 與x軸交于點F.
與x軸交于點F. ,
, AB•|yQ|=8×
AB•|yQ|=8× ,AB=3,|yQ|=8,yQ=±8.
,AB=3,|yQ|=8,yQ=±8. ,以及S△ABQ=
,以及S△ABQ= AB•|yQ|=8×
AB•|yQ|=8× ,AB=3,|yQ|=8,yQ=±8,即可得出Q點的坐標.
,AB=3,|yQ|=8,yQ=±8,即可得出Q點的坐標.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案