新活力總動員暑系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目：初中數學 來源：2014-2015學年河北省滄州市中考二模數學試卷（解析版） 題型：選擇題
計算：tan60°+2sin45°﹣2cos30°的結果是（ ）
A．2 B．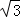
C．
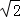D．1
查看答案和解析>>
科目：初中數學 來源：2014-2015學年山東省濰坊市中考三模數學試卷（解析版） 題型：選擇題
關于x的方程（a﹣6）x2﹣8x+6=0有實數根，則整數a的最大值是（ ）．
A．6 B．7 C．8 D．9
查看答案和解析>>
科目：初中數學 來源：2014-2015學年浙江省杭州市5月中考模擬數學試卷（解析版） 題型：選擇題
如圖，點A、B分別在射線OM、ON上，C、D分別是線段OA和OB上的點，以OC、OD為鄰邊作平行四邊形OCED，下面給出三種作法的條件：①取OC=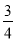
OA、OD=
OB； ②取OC=
OA、OD=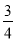OB；③取OC=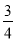OA、OD=
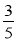OB．能使點E落在陰影區域內的作法有（ ）
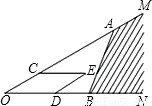
A．① B．①② C．①②③ D．②③
查看答案和解析>>
科目：初中數學 來源：2014-2015學年山東省威海市乳山市中考一模數學試卷（解析版） 題型：計算題
如圖1，將一個直角三角板的直角頂點P放在正方形ABCD的對角線BD上滑動，并使其一條直角邊始終經過點A，另一條直角邊與BC相交于點E．
（1）求證：PA=PE；
（2）若將（1）中的正方形變為矩形，其余條件不變（如圖2），且AD=10，DC=8，求AP：PE；
（3）在（2）的條件下，當P滑動到BD的延長線上時（如圖3），請你直接寫出AP：PE的比值．
【答案】（1）證明見解析；（2）AP：PE=5：4；（3）AP：PE=5：4；
【解析】
試題分析：（1）過P作PM⊥AB于M，PN⊥BC于N，四邊形BMPN是正方形，得出PM=PN，∠MPN=90°，求出∠APM=∠NPE，∠AMP=∠PNE，證△APM≌△EPN，推出AP=PE即可；
（2）證△BPM∽△BDA，△BNP∽△BCD，得出
，
，推出
，求出
，證△APM∽△EPN，推出
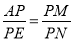即可；
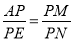（3）過P作PM⊥AB于M，PN⊥BC于N，證△BPM∽△BDA，△BNP∽△BCD，得出，，推出，求出，證△APM∽△EPN，推出即可．
試題解析：（1）證明：過P作PM⊥AB于M，PN⊥BC于N，
∵四邊形ABCD是正方形，
∴∠ABD=45°，
∴∠MPB=45°=∠ABD，
∴PM=BM，
同理BP=BN，
∵四邊形ABCD是正方形，
∴∠ABC=90°=∠BMP=∠BNP，
∴四邊形BMPN是正方形，
∴PM=PN，∠MPN=90°，
∵∠APE=90°，
∴都減去∠MPE得：∠APM=∠NPE，
∵PM⊥AB，PN⊥BC，
∴∠AMP=∠PNE，
在△APM和△EPN中
∴△APM≌△EPN（ASA），
∴AP=PE；
（2）【解析】
∵四邊形ABCD是矩形，
∴∠BAD=∠C=90°，
∵∠PMB=PNB=90°，
∴PM∥AD，PN∥CD，
∴△BPM∽△BDA，△BNP∽△BCD，
∴，，，
∴，
∴
，
∵∠AMP=∠ENP=90°，∠MPA=∠EPN，
∴△APM∽△EPN，
∴=
，
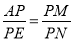AP：PE=5：4；
（3）【解析】
AP：PE=5：4．
考點：相似形綜合題．
【題型】解答題
【適用】一般
【標題】2015屆山東省威海市乳山市中考一模數學試卷（帶解析）
【關鍵字標簽】
【結束】
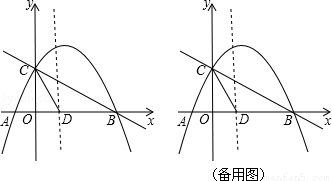
如圖，直線y=-
x+2與x軸交于點B，與y軸交于點C，已知二次函數的圖象經過點B，C和點A（-1，0）．
（1）求B，C兩點坐標；
（2）求該二次函數的關系式；
（3）若拋物線的對稱軸與x軸的交點為點D，點E是線段BC上的一個動點，過點E作x軸的垂線與拋物線相交于點F，當點E運動到什么位置時，四邊形CDBF的面積最大？求出四邊形CDBF的最大面積及此時E點的坐標；
（4）在拋物線的對稱軸上是否存在點P，使△PCD是以CD為腰的等腰三角形？如果存在，直接寫出P點的坐標；如果不存在，請說明問題．
查看答案和解析>>
科目：初中數學 來源：2014-2015學年山東省威海市乳山市中考一模數學試卷（解析版） 題型：填空題
在直角坐標系xOy中，對于點P（x，y），我們把點P′（y+1，-x+1）叫做點P的影子點．已知點A1的影子點為A2，點A2的影子點為A3，點A3的影子點為A4，…，這樣依次得到點A1，A2，A3，…，An，…若點A1的坐標為（a，b），對于任意的正整數n，點An均在y軸的右側，則a，b應滿足的條件是 ．
查看答案和解析>>
科目：初中數學 來源：2014-2015學年廣西省南寧市西鄉塘區中考二模數學試卷（解析版） 題型：選擇題
已知二次函數y=ax2+bx+c（a≠0）的圖象如圖所示，有下列結論：
①b2-4ac＞0；②abc＞0；③8a+c＞0；④9a+3b+c＜0
其中，正確結論的個數是（ ）
A．1 B．2 C．3 D．4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
．
）-1=（ ）