
【題目】已知:如圖,AB為![]() 的直徑,弦
的直徑,弦![]() 垂足為E,點H為弧AC上一點.連接DH交AB于點F,連接HA、BD,點G為DH上一點,連接AG,
垂足為E,點H為弧AC上一點.連接DH交AB于點F,連接HA、BD,點G為DH上一點,連接AG,![]() .
.
(1)如圖1,求證:![]() ;
;
(2)如圖2,連接HC,若![]() ,求證:
,求證:![]() ;
;
(3)如圖3,連接![]() 交
交![]() 于點K,若點F為DG的中點,
于點K,若點F為DG的中點,![]() ,求
,求![]() 的值.
的值.
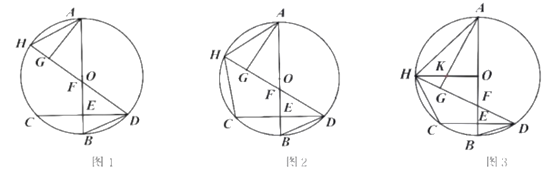
【答案】(1)詳見解析;(2)詳見解析;(3)![]()
【解析】
(1)根據同弧所對的圓周角相等,進行角度計算,得![]() ,進而得到
,進而得到![]() ,即可證明
,即可證明![]() ;
;
(2)連接AC、AD、CF,根據同弧所對的圓周角相等,進行角度計算,得![]() ,進而得到
,進而得到![]() ,再根據已知
,再根據已知![]() ,得到
,得到![]() ;
;
(3)在![]() 上截取
上截取![]() ,過點C作
,過點C作![]() 于點M,通過證明
于點M,通過證明![]() ≌
≌![]() 得到
得到![]() ,進而得到
,進而得到![]() ,再根據F為DG中點,得到
,再根據F為DG中點,得到![]() ,通過勾股定理逆用,證明
,通過勾股定理逆用,證明![]() ,再通過解
,再通過解![]() 得
得![]() ,解△CDH得
,解△CDH得![]() ,求得OF、OH,逆用勾股定理證明
,求得OF、OH,逆用勾股定理證明![]() ,易求
,易求![]() ,
,![]() ,最后求得
,最后求得![]() 的值.
的值.
(1)證明:如圖,設![]() 為
為![]() ,
,
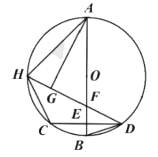
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() 與
與![]() 為同對弧
為同對弧![]() 所對的圓周角,
所對的圓周角,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
(2)如圖,連接AC、AD、CF,
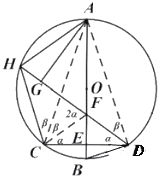
∵AB為直徑,![]() ,
,
∴![]() ,
,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
設![]() ,
,![]() ,
,
∵![]() 與
與![]() 為同對弧AH所對的圓周角,
為同對弧AH所對的圓周角,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB為直徑,
∴![]() ,
,
∴![]() ,
,
∵![]() 與為
與為![]() 同對弧BH所對的圓周角,
同對弧BH所對的圓周角,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)如圖,在![]() 上截取
上截取![]() ,
,
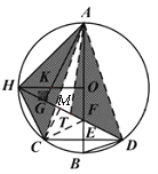
∵![]() 與
與![]() 同對弧AH所對的圓周角,
同對弧AH所對的圓周角,
∴![]() ,
,
∵AB為直徑,且![]()
∴![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,
,
∵F為DG中點,
∴![]() ,
,
∴![]() ,FD=CF=3k,
,FD=CF=3k,
在![]() 中,由勾股定理逆定理得
中,由勾股定理逆定理得![]() ,
,
過點C作![]() 于點M,
于點M,
由△HCF面積,可求CM=![]() ,
,
∴![]() ,
,
∴![]() ,
,
解![]() 得
得![]() ,
,
易求![]() ,
,![]() ,
,
由勾股定理逆定理得![]() ,
,
易求![]() ,
,![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】矩形ABCD中,E,F在BC、CD上,以EF為直徑的半圓切AD于G(如圖1).
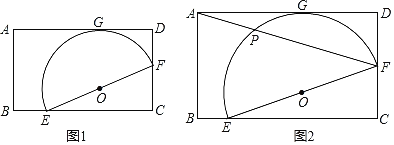
(1)求證:CE=2DG;
(2)若F為DC中點,連AF交半圓于P(如圖2),且AB=4,AD=5![]() ,求PF.
,求PF.
查看答案和解析>>
科目:初中數學 來源: 題型:
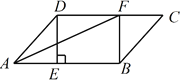
【題目】如圖,在平行四邊形![]() 中,過點
中,過點![]() 作
作![]() 于點
于點![]() ,點
,點![]() 在邊
在邊![]() 上,
上,![]() ,連接
,連接![]() ,
,![]() .
.
(1)求證:四邊形BFDE是矩形;
(2)若CF=3,BE=5,AF平分∠DAB,求平行四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中考體育測試前,某區教育局為了了解選報引體向上的初三男生的成績情況,隨機抽取了本區部分選報引體向上項目的初三男生的成績,并將測試得到的成績繪成了下面兩幅不完整的統計圖:

請你根據圖中的信息,解答下列問題:
(1)寫出扇形圖中![]() ______,并補全條形圖;
______,并補全條形圖;
(2)樣本數據的平均數是______,眾數是______,中位數是______;
(3)該區體育中考選報引體向上的男生共有1200人,如果體育中考引體向上達6個以上(含6個)得滿分,請你估計該區體育中考中選報引體向上的男生能獲得滿分的有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
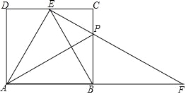
【題目】如圖,在矩形ABCD中,AB=2,AD=![]() ,在邊CD上有一點E,使EB平分∠AEC.若P為BC邊上一點,且BP=2CP,連接EP并延長交AB的延長線于F.給出以下五個結論:
,在邊CD上有一點E,使EB平分∠AEC.若P為BC邊上一點,且BP=2CP,連接EP并延長交AB的延長線于F.給出以下五個結論:
①點B平分線段AF;②PF=![]() DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
DE;③∠BEF=∠FEC;④S矩形ABCD=4S△BPF;⑤△AEB是正三角形.
其中正確結論的序號是.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分線,以AB上一點O為圓心,AD為弦作⊙O.
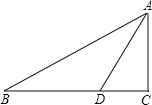
(1)用直尺和圓規在圖中作出⊙O(不寫作法,保留作圖痕跡),判斷直線BC與⊙O的位置關系,并說明理由;(友情提醒:必須作在答題卷上哦!)
(2)若AC=3,BC=4,求⊙O的半徑長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=![]() x+a與x軸交于點A(4,0),與y軸交于點B,拋物線y=
x+a與x軸交于點A(4,0),與y軸交于點B,拋物線y=![]() x2+bx+c經過點A,B.點M(m,0)為x軸上一動點,過點M且垂直于x軸的直線分別交直線AB及拋物線于點P,N.
x2+bx+c經過點A,B.點M(m,0)為x軸上一動點,過點M且垂直于x軸的直線分別交直線AB及拋物線于點P,N.
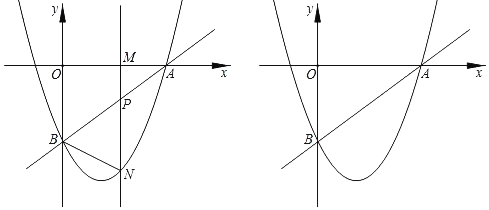
(1)填空:點B的坐標為 ,拋物線的解析式為 ;
(2)當點M在線段OA上運動時(不與點O,A重合),
①當m為何值時,線段PN最大值,并求出PN的最大值;②求出使△BPN為直角三角形時m的值;
(3)若拋物線上有且只有三個點N到直線AB的距離是h,請直接寫出此時由點O,B,N,P構成的四邊形的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com