
【題目】由于“新冠肺炎”的發(fā)生,市場上防護(hù)口罩出現(xiàn)熱銷.某藥店第一次用2000元購進(jìn)若干個防護(hù)口罩,并按定價2.5元/個出售,很快售完由于該防護(hù)口罩暢銷,第二次購進(jìn)時,每個防護(hù)口罩的進(jìn)價比第一次的進(jìn)價提高了25%,該藥店用3000元購進(jìn)防護(hù)口罩的數(shù)量比第一次多了200個,并把定價提高20%進(jìn)行銷售.
(1)第一次購進(jìn)時,每個防護(hù)口罩的價格是多少元?
(2)第二次售出800個防護(hù)口罩時,出現(xiàn)了滯銷,該藥店打算降價售完剩余的防護(hù)口罩.那么該藥店每個防護(hù)口罩至多降價多少元出售,才能使第二次銷售的防護(hù)口罩不虧本?
【答案】(1)第一次購進(jìn)時,每個防護(hù)口罩的價格是2元;(2)該藥店每個防護(hù)口罩至多降價1.5元銷售,才能使第二次銷售的防護(hù)口罩不虧本.
【解析】
(1)設(shè)第一次購進(jìn)時,每個防護(hù)口罩的價格是x元,則第二次購進(jìn)時,每個防護(hù)口罩的價格是(1+25%)x元,根據(jù)數(shù)量=總價÷單價結(jié)合第二次比第一次多購進(jìn)200個,即可得出關(guān)于x的分式方程,解之經(jīng)檢驗后即可得出結(jié)論;
(2)根據(jù)兩次進(jìn)貨單價間的關(guān)系可求出第二次購進(jìn)防護(hù)口罩的單價,結(jié)合數(shù)量=總價÷單價及定價比原價高20%,可求出第二次購進(jìn)防護(hù)口罩的數(shù)量及銷售單價,設(shè)該藥店每個防護(hù)口罩降價y元銷售,根據(jù)銷售總價=銷售單價×數(shù)量結(jié)合第二次銷售的防護(hù)口罩不虧本,即可得出關(guān)于y的一元一次不等式,解之取其中的最大值即可得出結(jié)論.
解:(1)設(shè)第一次購進(jìn)時,每個防護(hù)口罩的價格是x元,則第二次購進(jìn)時,每個防護(hù)口罩的價格是(1+25%)x元,
依題意,得:![]() ﹣
﹣![]() =200,
=200,
解得:x=2,
經(jīng)檢驗,x=2是原分式方程的解,且符合題意.
答:第一次購進(jìn)時,每個防護(hù)口罩的價格是2元.
(2)第二次購進(jìn)防護(hù)口罩的單價為(1+25%)×2=2.5(元),
第二次購進(jìn)防護(hù)口罩的數(shù)量為3000÷2.5=1200(個),
第二次購進(jìn)防護(hù)口罩的銷售單價為2.5×(1+20%)=3(元).
設(shè)該藥店每個防護(hù)口罩降價y元銷售,
依題意,得:800×3+(1200﹣800)(3﹣y)≥3000,
解得:y≤1.5.
答:該藥店每個防護(hù)口罩至多降價1.5元銷售,才能使第二次銷售的防護(hù)口罩不虧本.


 智慧小復(fù)習(xí)系列答案
智慧小復(fù)習(xí)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】觀察下列等式:
2+22=23﹣2;
2+22+23=24﹣2;
2+22+23+24=25﹣2;
2+22+23+24+25=26﹣2;
…
已知按一定規(guī)律排列的一組數(shù):220,221,222,223,224,…,238,239,240,若220=m,則220+221+222+223+224+…+238+239+240=_____(結(jié)果用含m的代數(shù)式表示).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】新龜兔賽跑的故事:龜兔從同一地點(diǎn)同時出發(fā)后,兔子很快把烏龜遠(yuǎn)遠(yuǎn)甩在后頭.驕傲自滿的兔子覺得自己遙遙領(lǐng)先,就躺在路邊呼呼大睡起來.當(dāng)它一覺醒來,發(fā)現(xiàn)烏龜已經(jīng)超過它,于是奮力直追,最后同時到達(dá)終點(diǎn).用S1、S2分別表示烏龜和兔子賽跑的路程,t為賽跑時間,則下列圖象中與故事情節(jié)相吻合的是( )
A.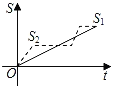 B.
B.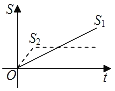
C.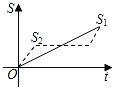 D.
D.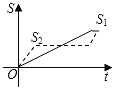
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
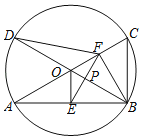
【題目】如圖,已知AC,BD為⊙O的兩條直徑,連接AB,BC,OE⊥AB于點(diǎn)E,點(diǎn)F是半徑OC的中點(diǎn),連接EF.
(1)設(shè)⊙O的半徑為1,若∠BAC=30°,求線段EF的長.
(2)連接BF,DF,設(shè)OB與EF交于點(diǎn)P,
①求證:PE=PF.
②若DF=EF,求∠BAC的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
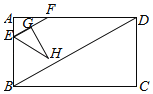
【題目】如圖,矩形ABCD中,AB=6,∠ABD=60°,點(diǎn)E從點(diǎn)A出發(fā),以每秒2個單位長度的速度沿邊AB運(yùn)動,到點(diǎn)B停止運(yùn)動.過點(diǎn)E作EF∥BD交AD于點(diǎn)F,將△AEF繞點(diǎn)E順時針旋轉(zhuǎn)得到△GEH,且點(diǎn)G落在線段EF上,設(shè)點(diǎn)E的運(yùn)動時間為t(秒)(0<t<3).
(1)若t=1,求△GEH的面積;
(2)若點(diǎn)G在∠ABD的平分線上,求BE的長;
(3)設(shè)△GEH與△ABD重疊部分的面積為T,用含t的式子表示T,并直接寫出當(dāng)0<t<3時T的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
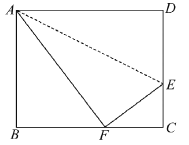
【題目】如圖,折疊矩形ABCD的一邊AD,使點(diǎn)D落在BC邊的點(diǎn)F處,已知折痕AE=5![]() cm, 且tan∠EFC=
cm, 且tan∠EFC=![]() ,那么矩形ABCD的周長_____________cm.
,那么矩形ABCD的周長_____________cm.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
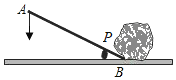
【題目】用杠桿撬石頭的示意圖如圖所示,P是支點(diǎn),當(dāng)用力壓杠桿的A端時,杠桿繞P點(diǎn)轉(zhuǎn)動,另一端B向上翹起,石頭就被撬動.現(xiàn)有一塊石頭要使其滾動,杠桿的B端必須向上翹起8cm,已知杠桿的動力臂AP與阻力臂BP之比為4:1,要使這塊石頭滾動,至少要將杠桿的A端向下壓_____cm.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某游泳館推出了兩種收費(fèi)方式.
方式一:顧客先購買會員卡,每張會員卡200元,僅限本人一年內(nèi)使用,憑卡游泳,每次游泳再付費(fèi)30元.
方式二:顧客不購買會員卡,每次游泳付費(fèi)40元.
設(shè)小亮在一年內(nèi)來此游泳館游泳的次數(shù)為![]() 次(
次(![]() 為正整數(shù)).
為正整數(shù)).
(1)根據(jù)題意,填寫下表:
游泳次數(shù) | 5 | 10 | 15 | … |
|
方式一的總費(fèi)用(元) | 350 | 650 | … | ||
方式二的總費(fèi)用(元) | 200 | 400 | … |
(2)若小亮計劃今年游泳的總費(fèi)用為2000元,選擇哪種付費(fèi)方式,他游泳的次數(shù)比較多;
(3)當(dāng)![]() 時,小亮選擇哪種付費(fèi)方式更合算.并說明理由.
時,小亮選擇哪種付費(fèi)方式更合算.并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ,交
,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() .
.
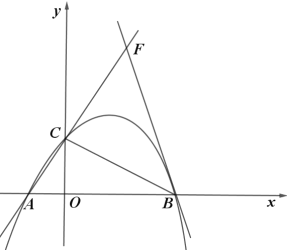
(1)求拋物線的函數(shù)表達(dá)式;
(2)點(diǎn)![]() 為
為![]() 軸右側(cè)拋物線上一點(diǎn),是否存在點(diǎn)
軸右側(cè)拋物線上一點(diǎn),是否存在點(diǎn)![]() 使
使![]() ?若存在,求出點(diǎn)
?若存在,求出點(diǎn)![]() 的坐標(biāo),若不存在,請說明理由.
的坐標(biāo),若不存在,請說明理由.
(3)將直線![]() 繞點(diǎn)
繞點(diǎn)![]() 順時針旋轉(zhuǎn)
順時針旋轉(zhuǎn)![]() ,與直線
,與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,求直線
,求直線![]() 的函數(shù)表達(dá)式.
的函數(shù)表達(dá)式.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com