
【題目】某縣實施“村村通”工程中,決定在A、B兩村之間修筑一條公路,甲、乙兩個工程隊分別從A、B兩村同時開始修筑,施工期間,乙隊因另有任務提前離開,余下的任務由甲隊單獨完成,直到道路修通,下圖是甲、乙兩個工程隊修道路長度y(米)與修筑時間x(天)之間的函數圖象,請根據圖象所提供的信息,解答下列問題:
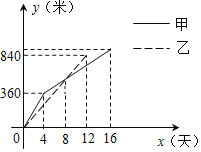
(1)寫出乙工程隊修道路的長度y與修筑時間x之間的函數關系式:_____;
(2)甲工程隊前8天所修公路為_____米,該公路的總長度為_____米;
(3)若乙工程隊不提前離開,則兩隊只需_____天就能完成任務;
(4)甲、乙兩工程隊第_____天時所修道路的長度相差80米.
【答案】y=70x 560 1800 13 4或12或![]()
【解析】
(1)設出正比例函數解析式,把(12,840)代入可得所求函數解析式;
(2)讓前4天修路的總路程除以4即可得到甲工程隊前4天平均每天修路米數,求得甲在第4天到第16天的函數解析式,進而求得后12天修路的總路程,除以12即為后12天平均修路的米數,進而得出甲工程隊前8天所修公路的路程;讓甲修路的總路程+乙修路的總路程即為公路的總長度;
(3)根據“工作總量=工作效率×工作時間”列式計算即可求解;
(4)根據題意列方程解答即可.
解:(1)設y=kx,
∵經過(12,840),
∴12k=840,
解得k=70,
∴y=70x,
故答案為y=70x;
(2)甲工程隊前4天平均每天修路米數為360÷4=90;
當x=8時,y=560,
設當4≤x≤16時,甲工程隊的函數解析式為y=kx+b,
![]() ,
,
解得![]() ,
,
∴y=50x+160,
當x=16時,y=960,
∴后12天平均每天修路米數為(960﹣360)÷12=50,
∴甲工程隊前8天所修公路為:360+50×(8﹣4)=560(米),
公路的總長度為840+960=1800(米),
故答案為560;1800
(3)若乙工程隊不提前離開,則兩隊需要的時間為:12+(1800﹣840×2)÷(50+70)=13(天).
故答案為:13;
(4)設甲、乙兩工程隊第x天時所修道路的長度相差80米,根據題意得
90x﹣70x=80或70x﹣[360+50(x﹣4)]=80或50(x﹣4)+360=840+80,
解得x=4或12或![]() .
.
故答案為:4或12或![]()


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源: 題型:
【題目】已知拋物線y=﹣![]() x2+bx+c經過點(1,0),(0,
x2+bx+c經過點(1,0),(0,![]() ).
).
(1)求該拋物線的函數表達式;
(2)將拋物線y=﹣![]() x2+bx+c平移,使其頂點恰好落在原點,請寫出一種平移的方法及平移后的函數表達式.
x2+bx+c平移,使其頂點恰好落在原點,請寫出一種平移的方法及平移后的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A、B兩點,與y軸交于點C,對稱軸為直線x=﹣1,點B的坐標為(1,0),則下列結論:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正確的結論有( )個.
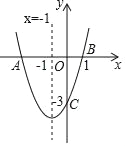
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中國是世界上13個貧水國家之一.某校有800名在校學生,學校為鼓勵學生節約用水,展開“珍惜水資源,節約每一滴水”系列教育活動.為響應學校號召,數學小組做了如下調查:
小亮為了解一個擰不緊的水龍頭的滴水情況,記錄了滴水時間和燒杯中的水面高度,如圖1.小明設計了調查問卷,在學校隨機抽取一部分學生進行了問卷調查,并制作出統計圖.如圖2和圖3.
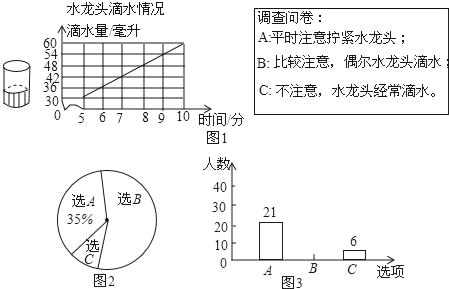
經結合圖2和圖3回答下列問題:
(1)參加問卷調查的學生人數為 人,其中選C的人數占調查人數的百分比為 .
(2)在這所學校中選“比較注意,偶爾水龍頭滴水”的大概有 人.若在該校隨機抽取一名學生,這名學生選B的概率為 .
請結合圖1解答下列問題:
(3)在“水龍頭滴水情況”圖中,水龍頭滴水量(毫升)與時間(分)可以用我們學過的哪種函數表示?請求出函數關系式.
(4)為了維持生命,每人每天需要約2400毫升水,該校選C的學生因沒有擰緊水龍頭,2小時浪費的水可維持多少人一天的生命需要?
查看答案和解析>>
科目:初中數學 來源: 題型:
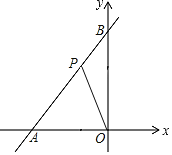
【題目】如圖,一次函數y=![]() x+4與x軸、y軸分別交于點A和點B,在線段AB上有一動點P(不與點A、B重合),連接OP,當點P的坐標為_____時線段OP最短.
x+4與x軸、y軸分別交于點A和點B,在線段AB上有一動點P(不與點A、B重合),連接OP,當點P的坐標為_____時線段OP最短.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小強每天堅持引體向上鍛煉,他記錄了某一周每天做引體向上的個數,如下表:

其中有三天的個數墨汁覆蓋了,但小強己經計算出這組數據唯一眾數是13,平均數是12,那么這組數據的方差是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
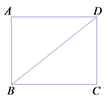
【題目】如圖,在矩形ABCD中,對角線BD的長為1,點P是線段BD上的一點,聯結CP,將△BCP沿著直線CP翻折,若點B落在邊AD上的點E處,且EP//AB,則AB的長等于________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰三角形ABC的底邊BC為4,面積為24,腰AC的垂直平分線EF分別交邊AC,AB于點E,F,若D為BC邊的中點,M為線段EF上一動點,則△CDM的周長的最小值為 ( )

A.8B.10C.12D.14
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】車間有20名工人,某天他們生產的零件個數統計如下表.
車間20名工人某一天生產的零件個數統計表
生產零件的個數(個) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人數(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求這一天20名工人生產零件的平均個數;
(2)為了提高大多數工人的積極性,管理者準備實行“每天定額生產,超產有獎”的措施.如果你是管理者,從平均數、中位數、眾數的角度進行分析,你將如何確定這個“定額”?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com