
【題目】如圖,已知拋物線經過原點O,頂點為A(1,1),且與直線y=x﹣2交于B,C兩點.
(1)求拋物線的解析式及點C的坐標;
(2)求證:△ABC是直角三角形;
(3)若點N為x軸上的一個動點,過點N作MN⊥x軸與拋物線交于點M,則是否存在以O,M,N為頂點的三角形與△ABC相似?若存在,請求出點N的坐標;若不存在,請說明理由.

【答案】(1)![]() ,C(﹣1,﹣3);(2)證明見解析;(3)(
,C(﹣1,﹣3);(2)證明見解析;(3)(![]() ,0)或(
,0)或(![]() ,0)或(﹣1,0)或(5,0).
,0)或(﹣1,0)或(5,0).
【解析】
(1)∵頂點坐標為(1,1),∴設拋物線解析式為![]() ,又拋物線過原點,∴
,又拋物線過原點,∴![]() ,解得a=﹣1,∴拋物線解析式為
,解得a=﹣1,∴拋物線解析式為![]() ,即
,即![]() ,聯立拋物線和直線解析式可得:
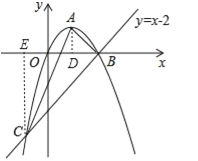
,聯立拋物線和直線解析式可得: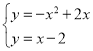 ,解得:
,解得:![]() 或
或![]() ,∴B(2,0),C(﹣1,﹣3);
,∴B(2,0),C(﹣1,﹣3);
(2)如圖,分別過A、C兩點作x軸的垂線,交x軸于點D、E兩點,則AD=OD=BD=1,BE=OB+OE=2+1=3,EC=3,∴∠ABO=∠CBO=45°,即∠ABC=90°,∴△ABC是直角三角形;
(3)假設存在滿足條件的點N,設N(x,0),則M(x,![]() ),∴ON=|x|,MN=
),∴ON=|x|,MN=![]() ,由(2)在Rt△ABD和Rt△CEB中,可分別求得AB=
,由(2)在Rt△ABD和Rt△CEB中,可分別求得AB=![]() ,BC=
,BC=![]() ,∵MN⊥x軸于點N
,∵MN⊥x軸于點N
∴∠ABC=∠MNO=90°,∴當△ABC和△MNO相似時,有![]() 或
或![]() ;
;
①當![]() 時,則有
時,則有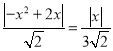 ,即
,即![]() ,∵當x=0時M、O、N不能構成三角形,∴x≠0,∴
,∵當x=0時M、O、N不能構成三角形,∴x≠0,∴![]() ,即
,即![]() ,解得x=
,解得x=![]() 或x=
或x=![]() ,此時N點坐標為(
,此時N點坐標為(![]() ,0)或(
,0)或(![]() ,0);
,0);
②當![]() 時,則有
時,則有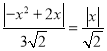 ,即
,即![]() ,∴|﹣x+2|=3,即﹣x+2=±3,解得x=5或x=﹣1,此時N點坐標為(﹣1,0)或(5,0);
,∴|﹣x+2|=3,即﹣x+2=±3,解得x=5或x=﹣1,此時N點坐標為(﹣1,0)或(5,0);
綜上可知存在滿足條件的N點,其坐標為(![]() ,0)或(
,0)或(![]() ,0)或(﹣1,0)或(5,0).
,0)或(﹣1,0)或(5,0).


科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,動點M從點B出發,在BA邊上以每秒2cm的速度向點A勻速運動,同時動點N從點C出發,在CB邊上以每秒![]() cm的速度向點B勻速運動,設運動時間為t秒(0≤t≤5),連接MN.
cm的速度向點B勻速運動,設運動時間為t秒(0≤t≤5),連接MN.
(1)若BM=BN,求t的值;
(2)若△MBN與△ABC相似,求t的值;
(3)當t為何值時,四邊形ACNM的面積最小?并求出最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某年級組織學生參加夏令營,分為甲、乙、丙三組進行活動.下面兩幅統計圖反映了學生報名參加夏令營的情況.請你根據圖中的信息回答下列問題:
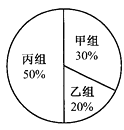
報名人數分布直方圖 報名人數扇形統計圖
(1)求該年級報名參加本次活動的總人數;
(2)求該年級報名參加乙組的人數,并補全頻數分布直方圖;
(3)根據實際情況,需從甲組抽調部分同學到丙組,使丙組人數是甲組人數的3倍,那么,應從甲組抽調多少名學生到丙組?
查看答案和解析>>
科目:初中數學 來源: 題型:
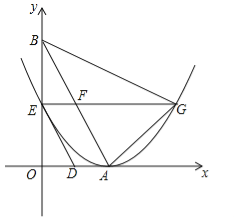
【題目】如圖,直線![]() 與x軸,y軸分別交于點A,點B,兩動點D,E分別從點A,點B同時出發向點O運動(運動到點O停止),運動速度分別是1個單位長度/秒和
與x軸,y軸分別交于點A,點B,兩動點D,E分別從點A,點B同時出發向點O運動(運動到點O停止),運動速度分別是1個單位長度/秒和![]() 個單位長度/秒,設運動時間為t秒,以點A為頂點的拋物線經過點E,過點E作x軸的平行線,與拋物線的另一個交點為點G,與AB相交于點F.
個單位長度/秒,設運動時間為t秒,以點A為頂點的拋物線經過點E,過點E作x軸的平行線,與拋物線的另一個交點為點G,與AB相交于點F.
(1)求點A,點B的坐標;
(2)用含t的代數式分別表示EF和AF的長;
(3)當四邊形ADEF為菱形時,試判斷△AFG與△AGB是否相似,并說明理由.
(4)是否存在t的值,使△AGF為直角三角形?若存在,求出這時拋物線的解析式;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果氣溫上升3度記作+3度,下降5度記作-5度,那么下列(1)+5度;(2)-6度; 各量分別表示什么?( )
A.上升5度;下降6度
B.上升6度;下降6度
C.上升5度;上升6度
D.下降5度;下降6度
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠1=∠2,要得到△ABD≌△ACD,還需從下列條件中補選一個,則錯誤的選法是( ) 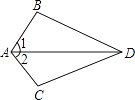
A.AB=AC
B.DB=DC
C.∠ADB=∠ADC
D.∠B=∠C
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】獲2019年度諾貝爾化學獎的“鋰電池”創造了一個更清潔的世界.我國新能源發展迅猛,某種特型鋰電池2016年銷售量為8萬個,到2018年銷售量為97萬個.設年均增長率為x,可列方程為( )
A.8(1+x)2=97B.97(1﹣x)2=8C.8(1+2x)=97D.8(1+x2)=97
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com