
【題目】已知:在平面直角坐標系![]() 中,對于任意的實數
中,對于任意的實數![]() ,直線
,直線![]() 都經過平面內一個定點
都經過平面內一個定點![]() .
.
(1)求點![]() 的坐標.
的坐標.
(2)反比例函數![]() 的圖象與直線
的圖象與直線![]() 交于點
交于點![]() 和另外一點
和另外一點![]()
①求![]() 的值;
的值;
②當![]() 時,求
時,求![]() 的取值范圍
的取值范圍
【答案】(1) A(-1,-2);(2)①b=2, m>0或m<-1.
【解析】
(1)解析式化為y=ax+a-2=a(x+1)-2,即可求得;
(2)①根據待定系數法即可求得;②根據反比例函數的性質即可判定點P(m,n)在第一象限或第三象限兩種情況,分別討論即可.
解:(1)∵y=ax+a-2=a(x+1)-2,
∴當x=-1時,y=-2,
∴直線y=ax+a-2都經過平面內一個定點A(-1,-2);
故答案為:A(-1,-2).
(2)①∵反比例函數![]() 的圖像經過點A,
的圖像經過點A,
∴b=-1×(-2)=2;
②若點P(m,n)在第一象限,當n>-2時,m>0,
若點P(m,n)在第三象限,當n>-2時,m<-1,
綜上,當n>-2時,m>0或m<-1.
故答案為:b=2,m的取值范圍是:m>0或m<-1.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
【題目】甲、乙、丙、丁四名同學進行一次乒乓球單打比賽,要從中選兩位同學打第一場比賽.
(1)若由甲挑一名選手打第一場比賽,選中乙的概率是 ;
(2)任選兩名同學打第一場,求恰好選中甲、乙兩位同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
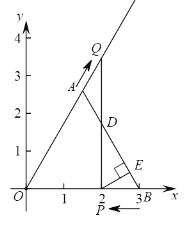
【題目】如圖,在平面直角坐標系xOy中,B(3,0),△AOB是等邊三角形,動點P從點B出發以每秒1個單位長度的速度沿BO勻速運動,動點Q同時從點A出發以同樣的速度沿OA延長線方向勻速運動,當點P到達點O時,點P,Q同時停止運動.過點P作PE⊥AB于E,連接PQ交AB于D.設運動時間為t秒,得出下面三個結論,① 當t =1時,△OPQ為直角三角形;② 當t =2時,以AQ,AE為邊的平行四邊形的第四個頂點在∠AOB的平分線上;③ 當t為任意值時,![]() .所有正確結論的序號是________.
.所有正確結論的序號是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
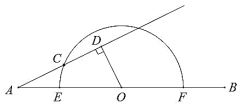
【題目】如圖,點![]() 是線段
是線段![]() 的中點,
的中點,![]() 是以
是以![]() 為圓心,
為圓心,![]() 長為直徑的半圓弧,點
長為直徑的半圓弧,點![]() 是
是![]() 上一動點,過點
上一動點,過點![]() 作射線
作射線![]() 的垂線,垂足為
的垂線,垂足為![]() .已知
.已知![]() ,
,![]() ,設
,設![]() 、
、![]() 兩點間的距離為
兩點間的距離為![]() ,
,![]() 、
、![]() 兩點間的距離為
兩點間的距離為![]() ,
,![]() 、
、![]() 兩點間的距離為
兩點間的距離為![]() .
.
小麗根據學習函數的經驗,分別對函數![]() 和
和![]() 隨自變量
隨自變量![]() 變化而變化的規律進行了探究.下面是小麗的探究過程,請將它補充完整:
變化而變化的規律進行了探究.下面是小麗的探究過程,請將它補充完整:
(1)按照下表中自變量![]() 的值進行取點、畫圖、測量,分別得到
的值進行取點、畫圖、測量,分別得到![]() 和
和![]() 與
與![]() 的幾組對應值:
的幾組對應值:
| 2 | 3 | 4 | 4.5 | 5 | 5.5 | 6 | 7 | 8 |
| 0 | 2.76 |
| 2.96 | 2.86 | 2.70 | 2.49 | 1.85 | 0 |
| 3.00 | 1.18 | 0 | 0.47 | 0.90 | 1.30 | 1.37 | 2.36 | 3.00 |
經測量,![]() 的值是______;(保留一位小數)
的值是______;(保留一位小數)
(2)在同一平面直角坐標系![]() 中,描出補全后的表中各組數值所對應的點
中,描出補全后的表中各組數值所對應的點![]() 和
和![]() ,并畫出函數
,并畫出函數![]() 、
、![]() 的圖象;
的圖象;
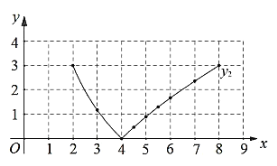
(3)結合函數圖象,解決問題:連接![]() ,當
,當![]() 是等腰三角形時,
是等腰三角形時,![]() 的長度約為______
的長度約為______![]() .(結果保留一位小數)
.(結果保留一位小數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 為平面內不在同一直線上的三點,點
為平面內不在同一直線上的三點,點![]() 為平面內一個動點,線段
為平面內一個動點,線段![]() 的中點分別為
的中點分別為![]() .在點
.在點![]() 的運動過程中,有下列結論:①存在無數個中點四邊形
的運動過程中,有下列結論:①存在無數個中點四邊形![]() 是平行四邊形;②存在無數個中點四邊形
是平行四邊形;②存在無數個中點四邊形![]() 是菱形;③存在無數個中點四邊形
是菱形;③存在無數個中點四邊形![]() 是矩形;④存在兩個中點四邊形
是矩形;④存在兩個中點四邊形![]() 是正方形.所有正確結論的序號是________.
是正方形.所有正確結論的序號是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】改革開放以來,人們的支付方式發生了巨大轉變,近年來,移動支付已成為主要的支付方式之一,為了解某校學生上個月![]() 兩種移動支付方式的使用情況,從全校
兩種移動支付方式的使用情況,從全校![]() 名學生中隨機抽取了
名學生中隨機抽取了![]() 人,發現樣本中
人,發現樣本中![]() 兩種支付方式都不使用的有
兩種支付方式都不使用的有![]() 人,樣本中僅使用
人,樣本中僅使用![]() 種支付方式和僅使用
種支付方式和僅使用![]() 種支付方式的學生的支付金額
種支付方式的學生的支付金額![]() (元)的分布情況如下:
(元)的分布情況如下:
支付金額 支付方式 |
|
|
|
僅使用 |
|
|
|
僅使用 |
|
|
|
下面有四個推斷:
①從樣本中使用移動支付的學生中隨機抽取一名學生,該生使用A支付方式的概率大于他使用B支付方式的概率;
②根據樣本數據估計,全校1000名學生中.同時使用A、B兩種支付方式的大約有400人;
③樣本中僅使用A種支付方式的同學,上個月的支付金額的中位數一定不超過1000元;
④樣本中僅使用B種支付方式的同學,上個月的支付金額的平均數一定不低于1000元.其中合理的是( )
A.①③B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
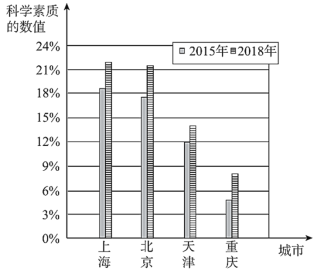
【題目】國務院發布的《全民科學素質行動計劃綱要實施方案(2016-2020年)》指出:公民科學素質是實施創新驅動發展戰略的基礎,是國家綜合國力的體現.《方案》明確提出,2020年要將我國公民科學素質的數值提升到10%以上.為了解我國公民科學素質水平及發展狀況,中國科協等單位已多次組織了全國范圍的調查,以下是根據調查結果整理得到的部分信息.注:科學素質的數值是指具備一定科學素質的公民人數占公民總數的百分比.
![]() .2015和2018年我國各直轄市公民科學素質發展狀況統計圖如下:
.2015和2018年我國各直轄市公民科學素質發展狀況統計圖如下:
b.2015年和2018年我國公民科學素質發展狀況按性別分類統計如下:
2015年 | 2018年 | |
男 |
|
|
女 |
|
|
c.2001年以來我國公民科學素質水平發展統計圖如下:
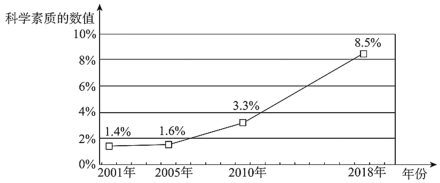
根據以上信息,回答下列問題:
(1)在我國四個直轄市中,從2015年到2018年,公民科學素質水平增幅最大的城市是________,公民科學素質水平增速最快的城市是_________.注:科學素質水平增幅=2018年科學素質的數值一2015年科學素質的數值;科學素質水平增速=(2018年科學素質的數值一2015年科學素質的數值)÷2015年科學素質的數值.
(2)已知在2015年的調查樣本中,男女公民的比例約為1:1,則2015年我國公民的科學素質水平為______%(結果保留一位小數);由計算可知.在2018年的調查樣本中.男性公民人數_____女性公民人數(填“多于”、“等于”或“少于”).
(3)根據截至2018年的調查數據推斷,你認為“2020年我國公民科學素質提升到10%以上”的目標能夠實現嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C是![]() 上的一定點,P是弦AB上的一動點,連接PC,過點A作AQ⊥PC交直線PC于點Q.小石根據學習函數的經驗,對線段PC,PA,AQ的長度之間的關系進行了探究.(當點P與點A重合時,令AQ=0cm)
上的一定點,P是弦AB上的一動點,連接PC,過點A作AQ⊥PC交直線PC于點Q.小石根據學習函數的經驗,對線段PC,PA,AQ的長度之間的關系進行了探究.(當點P與點A重合時,令AQ=0cm)
下面是小石的探究過程,請補充完整:
(1)對于點P在弦AB上的不同位置,畫圖、測量,得到了線段PC,PA,AQ的幾組值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
PC/cm | 4.07 | 3.10 | 2.14 | 1.68 | 1.26 | 0.89 | 0.76 | 1.26 | 2.14 |
PA/cm | 0.00 | 1.00 | 2.00 | 2.50 | 3.00 | 3.54 | 4.00 | 5.00 | 6.00 |
AQ/cm | 0.00 | 0.25 | 0.71 | 1.13 | 1.82 | 3.03 | 4.00 | 3.03 | 2.14 |
在PC,PA,AQ的長度這三個量中,確定 的長度是自變量, 的長度和 的長度都是這個自變量的函數;
(2)在同一平面直角坐標系xOy中,畫出(1)中所確定的函數的圖象;
(3)結合函數圖象,解決問題:當AQ=PC時,PA的長度約為 cm.(結果保留一位小數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形ABCD中,AB=5,BC=4,E是BC邊上一點,連接DE,將矩形ABCD沿DE折疊,頂點C恰好落在AB邊上點F處,延長DE交AB的延長線于點G.
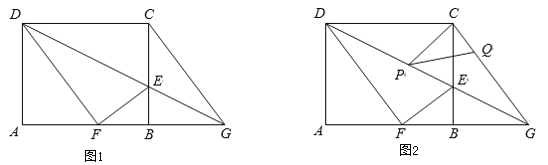
(1)求線段BE的長;
(2)連接CG,求證:四邊形CDFG是菱形;
(3)如圖2,P,Q分別是線段DG,CG上的動點(與端點不重合),且∠CPQ=∠CDP,是否存在這樣的點P,使△CPQ是等腰三角形?若存在,請直接寫出DP的值,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com