

 ×DE×OA列出方程,解方程求出a的值,即可確定拋物線的解析式;
×DE×OA列出方程,解方程求出a的值,即可確定拋物線的解析式; .設y=-x2-2x+3=-(x+1)2+4向右平移后的拋物線解析式為y=-(x+m)2+4,兩條拋物線交于點P,直線AP與y軸交于點F.根據正切函數的定義求出OF=1.分兩種情況進行討論:(Ⅰ)如圖2①,F點的坐標為(0,1),(Ⅱ)如圖2②,F點的坐標為(0,-1).針對這兩種情況,都可以先求出點P的坐標,再得出m的值,進而求出平移后拋物線的解析式.
.設y=-x2-2x+3=-(x+1)2+4向右平移后的拋物線解析式為y=-(x+m)2+4,兩條拋物線交于點P,直線AP與y軸交于點F.根據正切函數的定義求出OF=1.分兩種情況進行討論:(Ⅰ)如圖2①,F點的坐標為(0,1),(Ⅱ)如圖2②,F點的坐標為(0,-1).針對這兩種情況,都可以先求出點P的坐標,再得出m的值,進而求出平移后拋物線的解析式.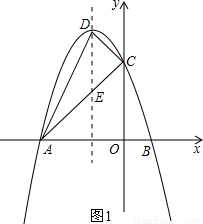 (2)如圖1,①設AC與拋物線對稱軸的交點為E.
(2)如圖1,①設AC與拋物線對稱軸的交點為E.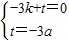 ,
,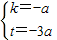 ,
, ×DE×OA=
×DE×OA= ×(-2a)×3=-3a,
×(-2a)×3=-3a,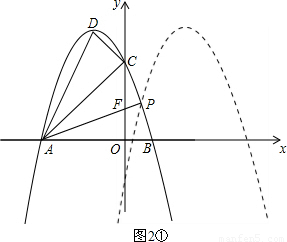 ∵A(-3,0),
∵A(-3,0),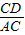 =
=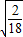 =
= ,
, .
.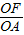 =
=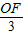 =
= ,
, x+1,
x+1, ,解得
,解得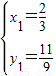 ,
,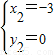 (舍去),
(舍去), ,
,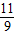 ),
), ,
, )代入y=-(x+m)2+4,
)代入y=-(x+m)2+4,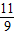 =-(
=-( +m)2+4,
+m)2+4, ,m2=1(舍去),
,m2=1(舍去), )2+4;
)2+4; (Ⅱ)如圖2②,當F點的坐標為(0,-1)時,易求直線AF的解析式為y=-
(Ⅱ)如圖2②,當F點的坐標為(0,-1)時,易求直線AF的解析式為y=- x-1,
x-1,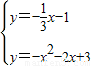 ,解得
,解得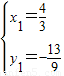 ,
,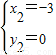 (舍去),
(舍去), ,-
,-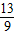 ),
), ,-
,-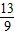 )代入y=-(x+m)2+4,
)代入y=-(x+m)2+4,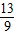 =-(
=-( +m)2+4,
+m)2+4,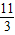 ,m2=1(舍去),
,m2=1(舍去),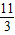 )2+4;
)2+4; )2+4或y=-(x-
)2+4或y=-(x-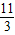 )2+4.
)2+4.

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 9 |
| 8 |
 兩點,試問當x為何值時,線段CD有最大值,其最大值為多少?
兩點,試問當x為何值時,線段CD有最大值,其最大值為多少?查看答案和解析>>
科目:初中數學 來源: 題型:
 O為坐標原點,拋物線上一點C的橫坐標為1.
O為坐標原點,拋物線上一點C的橫坐標為1.查看答案和解析>>
科目:初中數學 來源: 題型:
 此拋物線上,矩形面積為12,
此拋物線上,矩形面積為12,查看答案和解析>>
科目:初中數學 來源: 題型:
 與x軸交于點A、B,點A的坐標為(-2,0).
與x軸交于點A、B,點A的坐標為(-2,0).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com