
【題目】問題背景
如圖![]() ,在正方形
,在正方形![]() 的內部,作
的內部,作![]() ,根據三角形全等的條件,易得
,根據三角形全等的條件,易得![]() ≌
≌![]() ≌
≌![]() ≌
≌![]() ,從而得到四邊形
,從而得到四邊形![]() 是正方形.
是正方形.
類比探究
如圖![]() ,在正
,在正![]() 的內部,作
的內部,作![]() ,
, ![]() ,
, ![]() ,
, ![]() 兩兩相交于
兩兩相交于![]() ,
, ![]() ,
, ![]() 三點(
三點(![]() ,
, ![]() ,
, ![]() 三點不重合).
三點不重合).
(![]() )
)![]() ,
, ![]() ,
, ![]() 是否全等?如果是,請選擇其中一對進行證明.
是否全等?如果是,請選擇其中一對進行證明.
(![]() )
)![]() 是否為正三角形?請說明理由.
是否為正三角形?請說明理由.
(![]() )進一步探究發現,圖
)進一步探究發現,圖![]() 中的
中的![]() 的三邊存在一定的等量關系,設
的三邊存在一定的等量關系,設![]() ,
, ![]() ,
, ![]() ,請探索
,請探索![]() ,
, ![]() ,
, ![]() 滿足的等量關系.
滿足的等量關系.


【答案】(1)見解析;(2)是;(3)![]()
【解析】試題分析:(1)由正三角形的性質得出∠CAB=∠ABC=∠BCA=60°,AB=BC,證出∠ABD=∠BCE,由ASA證明△ABD≌△BCE即可;
(2)由全等三角形的性質得出∠ADB=∠BEC=∠CFA,證出∠FDE=∠DEF=∠EFD,即可得出結論;
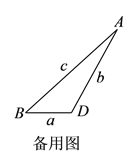
(3)作AG⊥BD于G,由正三角形的性質得出∠ADG=60°,在Rt△ADG中,DG=![]() b,AG=
b,AG=![]() b,在Rt△ABG中,由勾股定理即可得出結論.
b,在Rt△ABG中,由勾股定理即可得出結論.
試題解析:( ![]() )
)![]() ≌
≌![]() ≌
≌![]() ,理由如下:
,理由如下:
∵![]() 是正三角形,
是正三角形,
∴![]() ,
, ![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,  ,
,
∴![]() ≌
≌![]() ,
,
同理可得![]() ≌
≌![]() ,
,
∴![]() ≌
≌![]() ≌
≌![]() .
.
(![]() )
)![]() 是正三角形,理由如下.
是正三角形,理由如下.
∵![]() ≌
≌![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是正三角形.
是正三角形.
(![]() )作
)作![]() 于
于![]() ,如圖所示:
,如圖所示:

∵![]() 是正三角形,
是正三角形,
∴![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
在![]() 中,
中, 
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】按照下列要求畫圖并填空:
(1)過點![]() 畫出直線
畫出直線![]() 的垂線,交直線
的垂線,交直線![]() 于點
于點![]() ,那么點
,那么點![]() 到直線
到直線![]() 的距離是線段______________的長.
的距離是線段______________的長.
(2)作出△![]() 的邊
的邊![]() 的垂直平分線
的垂直平分線![]() ,分別交邊
,分別交邊![]() 、
、![]() 于點
于點![]() 、
、![]() ,聯結
,聯結![]() ,那么線段
,那么線段![]() 是△
是△![]() 的______________.(保留作圖痕跡)
的______________.(保留作圖痕跡)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 要了解某公司生產的100萬只燈泡的使用壽命,可以采用抽樣調查的方法
B. 4位同學的數學期末成績分別為100、95、105、110,則這四位同學數學期末成績的中位數為100
C. 甲乙兩人各自跳遠10次,若他們跳遠成績的平均數相同,甲乙跳遠成績的方差分別為0.51和0.62
D. 某次抽獎活動中,中獎的概率為![]() 表示每抽獎50次就有一次中獎
表示每抽獎50次就有一次中獎
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的角平分線CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列結論:
①∠CEG=2∠DCB;②∠DFB=![]() ∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正確的個數是( )
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正確的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店用1000元人民幣購進水果銷售,過了一段時間,又用2400元人民幣購進這種水果,所購數量是第一次購進數量的2倍,但每千克的價格比第一次購進的貴了2元.
(1)該商店第一次購進水果多少千克?
(2)假設該商店兩次購進的水果按相同的標價銷售,最后剩下的20千克按標價的五折優惠銷售.若兩次購進水果全部售完,利潤不低于950元,則每千克水果的標價至少是多少元?
注:每千克水果的銷售利潤等于每千克水果的銷售價格與每千克水果的購進價格的差,兩批水果全部售完的利潤等于兩次購進水果的銷售利潤之和.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一只不透明的袋子中裝有2個白球和1個紅球,這些球除顏色外都相同,攪勻后從中任意摸出1個球(不放回),再從余下的2個球中任意摸出1個球.
(1)用樹狀圖或列表等方法列出所有可能出現的結果;
(2)求兩次摸到的球的顏色不同的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖(1),已知任意三角形ABC,過點C作DE∥AB;
①求證:∠DCA=∠A; ②求證:∠A+∠B+∠ACB=180°;
(2)如圖(2),求證:∠AGF=∠AEF+∠F;
(3)如圖(3),AB∥CD,∠CDE=119°,GF交∠DEB的平分線EF于點F,∠AGF=150°,求∠F.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com