
【題目】已知:如圖所示,![]() 是
是![]() 的直徑,
的直徑,![]() 是
是![]() 上一點,
上一點,![]() 平分
平分![]() 交
交![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() .
.
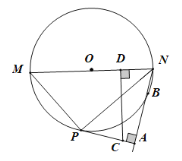
(1)求證:![]() 與
與![]() 相切;
相切;
(2)若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(3)若![]() 是
是![]() 中點,過
中點,過![]() 作
作![]() 交
交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的半徑.
的半徑.
【答案】(1)見解析; (2)![]() ;(3)半徑
;(3)半徑![]()
【解析】
(1)連接OP,根據角平分線的性質及圓的半徑相等的性質得到![]() ,推出OP∥AN,根據
,推出OP∥AN,根據![]() 即可得到OP⊥PA,由此得到結論;
即可得到OP⊥PA,由此得到結論;
(2)連接![]() 交
交![]() 于
于![]() ,根據勾股定理求出BM=16得到ME=8,再利用勾股定理求出OE=6,得到PE=4,即可利用勾股定理求出MP;
,根據勾股定理求出BM=16得到ME=8,再利用勾股定理求出OE=6,得到PE=4,即可利用勾股定理求出MP;
(3)連接![]() ,設
,設![]() 與
與![]() 的交點為
的交點為![]() ,根據
,根據![]() 設
設![]() ,可求
,可求![]() ,根據角平分線的性質及圓的半徑相等的性質得到
,根據角平分線的性質及圓的半徑相等的性質得到![]() ,推出PC=FC,根據
,推出PC=FC,根據![]() 求出x=2,即可得到半徑OP.
求出x=2,即可得到半徑OP.
(1)證明:連接![]() .
.
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]() 與
與![]() 相切;
相切;
(2)解:連接![]() 交
交![]() 于
于![]() ,
,
∵MN是直徑,
∴BM⊥BN,
∴OP⊥BM,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)解:連接![]() ,設
,設![]() 與
與![]() 的交點為
的交點為![]() .
.
![]() ,
,
∴可設![]() ,
,
![]() .
.
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
∴半徑![]() .
.


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,∠BAD的平分線交BC于點E,交DC的延長線于點F,取EF的中點G,連接CG、BG、DG,下列結論中錯誤的是( )
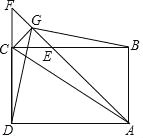
A.BC=DFB.△DCG≌△BGCC.△DFG≌△BCGD.AC:BG=![]() :1
:1
查看答案和解析>>
科目:初中數學 來源: 題型:
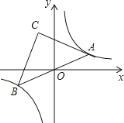
【題目】如圖,點A是雙曲線![]() 在第一象限上的一動點,連接AO并延長交另一分支于點B,以AB為斜邊作等腰Rt△ABC,點C在第二象限,隨著點A的運動,點C的位置也不斷的變化,但始終在一函數圖象上運動,則這個函數的解析式為 .
在第一象限上的一動點,連接AO并延長交另一分支于點B,以AB為斜邊作等腰Rt△ABC,點C在第二象限,隨著點A的運動,點C的位置也不斷的變化,但始終在一函數圖象上運動,則這個函數的解析式為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
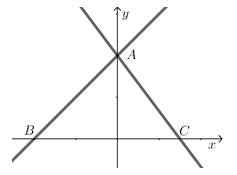
【題目】如圖,在平面直角坐標系中,直線y=x+4與y軸交于點A,與x軸交于點B,直線y=kx+b經過點A,且交x軸與點C(3,0).
(1)求直線AC的函數表達式;
(2)動點P在線段CB上由C向B勻速運動,到達點B后停止運動,運動速度為3個單位長度,過點P作PE⊥x軸,交直線AC于點E,過點E作直線GE∥x軸交![]() 軸于點F,交直線AB于點G,設點P的運動時間為t(t>0)秒.
軸于點F,交直線AB于點G,設點P的運動時間為t(t>0)秒.
①直接寫出線段PE的長度(用含t的代數式表示);
②當EG=1時,請直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 、
、![]() 是反比例函數
是反比例函數![]()
![]() 圖象上的點,
圖象上的點,![]() 于點
于點![]() ,
,![]() .
.
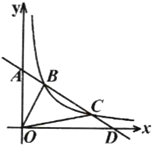
(1)求直線![]() 的函數解析式及反比例函數的解析式;
的函數解析式及反比例函數的解析式;
(2)若![]() 、
、![]() 、
、![]() 的面積分別為
的面積分別為![]() ,
,![]() ,
,![]() ,直接寫出
,直接寫出![]() ,
,![]() ,
,![]() 的一個數量關系式.
的一個數量關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題引入:如圖1所示,正方形![]() 和正方形
和正方形![]() ,則
,則![]() 與
與![]() 的數量關系是 ,
的數量關系是 ,![]() ;
;
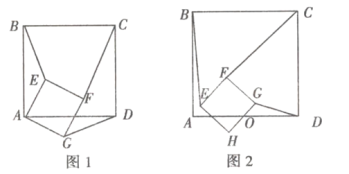
(2)類比探究:如圖2所示,![]() 為
為![]() 、
、![]() 的中點,正方形
的中點,正方形![]() 和正方形
和正方形![]() 中,判斷
中,判斷![]() 和
和![]() 的數量關系,并求出
的數量關系,并求出![]() 的值.
的值.
(3)解決問題:
①若把(1)中的正方形都改成矩形,且![]() ,則(1)中的結論還成立嗎?若不能成立,請寫出
,則(1)中的結論還成立嗎?若不能成立,請寫出![]() 與
與![]() 的關系,并求出
的關系,并求出![]() 的值;
的值;
②若把(2)中的正方形也都改成矩形,且![]() ,請直接寫出
,請直接寫出![]() 和
和![]() 的關系以及
的關系以及![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() (
(![]() )的頂點為
)的頂點為![]() ,對稱軸與
,對稱軸與![]() 軸交于點
軸交于點![]() ,當以
,當以![]() 為對角線的正方形
為對角線的正方形![]() 的另外兩個頂點
的另外兩個頂點![]() 、
、![]() 恰好在拋物線上時,我們把這樣的拋物線稱為美麗拋物線,正方形
恰好在拋物線上時,我們把這樣的拋物線稱為美麗拋物線,正方形![]() 為它的內接正方形.
為它的內接正方形.
(1)當拋物線![]() 是美麗拋物線時,則
是美麗拋物線時,則![]() ______;當拋物線
______;當拋物線![]() 是美麗拋物線時,則
是美麗拋物線時,則![]() ______;
______;
(2)若拋物線![]() 是美麗拋物線時,則請直接寫出
是美麗拋物線時,則請直接寫出![]() ,
,![]() 的數量關系;
的數量關系;
(3)若![]() 是美麗拋物線時,(2)
是美麗拋物線時,(2)![]() ,
,![]() 的數量關系成立嗎?為什么?
的數量關系成立嗎?為什么?
(4)系列美麗拋物線![]() (
(![]() 為小于
為小于![]() 的正整數)頂點在直線
的正整數)頂點在直線![]() 上,且它們中恰有兩條美麗拋物線內接正方形面積比為
上,且它們中恰有兩條美麗拋物線內接正方形面積比為![]() .求它們二次項系數之和.
.求它們二次項系數之和.
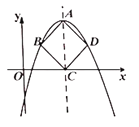
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在電線桿CD上的C處引拉線CE、CF固定電線桿,拉線CE和地面所成的角∠CED=60°,在離電線桿9m的B處安置高為1.5m的測角儀AB,在A處測得電線桿上C處的仰角為30°,求拉線CE的長.(結果保留根號)
![]()
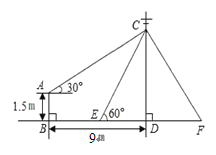
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若干名工人某天生產同一種玩具,生產的玩具數整理成條形圖(如圖所示).則他們生產的玩具數的平均數、中位數、眾數分別為( )

A.5,5,4 B.5,5,5
C.5,4,5 D.5,4,4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com