
 AD=
AD= DE,再根據直角三角形的性質得出∠EDA=30°,由銳角三角函數的定義得到AE的長,利用三角形的面積公式即可得出結論;
DE,再根據直角三角形的性質得出∠EDA=30°,由銳角三角函數的定義得到AE的長,利用三角形的面積公式即可得出結論; =
=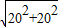 =20
=20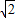 cm;
cm; AD=
AD= DF
DF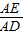 ,
,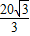
 AE•AD=
AE•AD= ×20×
×20× =
=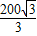 ;
;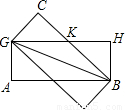 (3)最大的菱形如圖所示:
(3)最大的菱形如圖所示: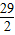 ,
,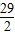 ×10=145.
×10=145.

科目:初中數學 來源: 題型:
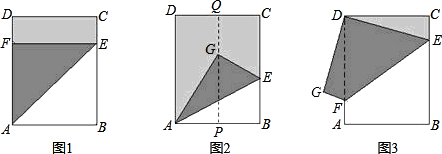
查看答案和解析>>
科目:初中數學 來源: 題型:
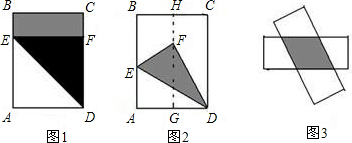
查看答案和解析>>
科目:初中數學 來源:第25章《圖形的變換》常考題集(25):25.3 軸對稱變換(解析版) 題型:解答題
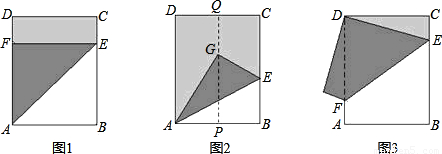
查看答案和解析>>
科目:初中數學 來源:2009-2010學年浙江省杭州市九年級(上)期末數學模擬試卷02(解析版) 題型:解答題
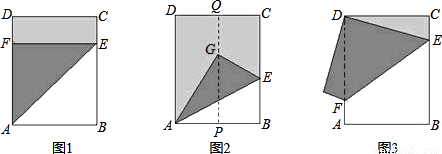
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com