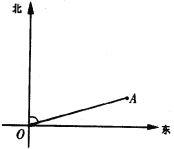
【題目】如圖，燈塔A周圍1000米水域內有礁石，一艦艇由西向東航行，在O處測得燈塔A在北偏東74°方向線上，這時O、A相距4200米，如果不改變航向，此艦艇是否有觸礁的危險？(指定數學課使用科學計算器的地區的考生須使用計算器計算．以下數據供計算器未進入考場的地區的考生選用：cos74°＝0.2756，sin74°＝0.9613，cot74°＝0.2867，tan74°＝3.487)
閱讀快車系列答案科目：初中數學 來源： 題型：
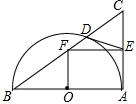
【題目】如圖，以Rt△ABC的直角邊AB為直徑作半圓⊙O與邊BC交于點D，過D作半圓的切線與邊AC交于點E，過E作EF∥AB，與BC交于點F．若AB＝20，OF＝7.5，則CD的長為（ ）
A.7B.8C.9D.10
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】設直線y＝kx+6和直線y＝（k+1）x+6（k是正整數）及x軸圍成的三角形面積為Sk（k＝1，2，3，…，8），則S1+S2+S3+…+S8的值是（ ）
A. 
B. 
C. 16D. 14
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在正方形ABCD中，對角線AC，BD交于點O，點P在線段BC上（不含點B），∠BPE＝
∠ACB，PE交BO于點E，過點B作BF⊥PE，垂足為F，交AC于點G．
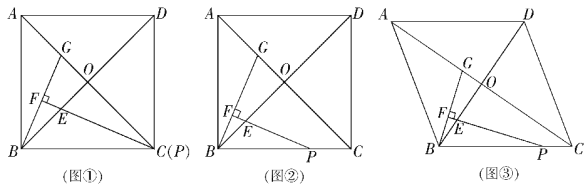
（1） 當點P與點C重合時（如圖①）．求證：△BOG≌△POE；（4分）
（2）通過觀察、測量、猜想：
= ，并結合圖②證明你的猜想；（5分）
（3）把正方形ABCD改為菱形，其他條件不變（如圖③），若∠ACB=α，求的值．（用含α的式子表示）（5分）
查看答案和解析>>
科目：初中數學 來源： 題型：
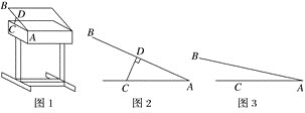
【題目】某課桌生產廠家研究發現，傾斜12°～24°的桌面有利于學生保持軀體自然姿勢．根據這一研究，廠家決定將水平桌面做成可調節角度的桌面．新桌面的設計圖如圖1，AB可繞點A旋轉，在點C處安裝一根可旋轉的支撐臂CD，AC＝30 cm.
(1)如圖2，當∠BAC＝24°時，CD⊥AB，求支撐臂CD的長；
(2)如圖3，當∠BAC＝12°時，求AD的長．(結果保留根號)
(參考數據：sin 24°≈0.40，cos 24°≈0.91，tan 24°≈0.46，sin 12°≈0.20)
查看答案和解析>>
科目：初中數學 來源： 題型：
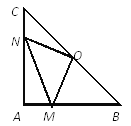
【題目】在Rt△ABC中，AB＝AC，∠BAC=90°，O為BC的中點。
（1）寫出點O到△ABC的三個頂點A、B、C的距離的大小關系并說明理由；
（2）如果點M、N分別在線段AB、AC上移動，在移動中保持AN＝BM，請判斷△OMN的形狀，并證明你的結論。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明的書包里只放了A4大小的試卷共4張，其中語文1張、數學2張、英語1張
若隨機地從書包中抽出2張，求抽出的試卷中有英語試卷的概率．
若隨機地從書包中抽出3張，抽出的試卷中有英語試卷的概率為______
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，點E在對角線BD上，EF∥AB交AD于點F，連接BF．
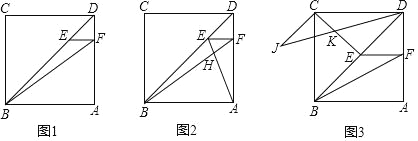
（1）如圖1，若AB＝4，DE＝
，求BF的長；
（2）如圖2．連接AE，交BF于點H，若DF＝HF＝2，求線段AB的長；
（3）如圖3，連接BF，AB＝3，設EF＝x，△BEF的面積為S，請用x的表達式表示S，并求出S的最大值；當S取得最大值時，連接CE，線段DB繞點D順時針旋轉30°得到線段DJ，DJ與CE交于點K，連接CJ，求證：CJ⊥CE．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，拋物線y=ax2+bx+c（a＜0）與x軸交于A（﹣2，0）、B（4，0）兩點，與y軸交于點C，且OC=2OA．
（1）試求拋物線的解析式；
（2）直線y=kx+1（k＞0）與y軸交于點D，與拋物線交于點P，與直線BC交于點M，記m=
，試求m的最大值及此時點P的坐標；
（3）在（2）的條件下，點Q是x軸上的一個動點，點N是坐標平面內的一點，是否存在這樣的點Q、N，使得以P、D、Q、N四點組成的四邊形是矩形？如果存在，請求出點N的坐標；如果不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
