
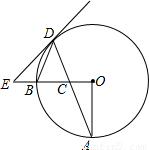
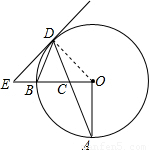
 解:(1)證明:連結OD,
解:(1)證明:連結OD,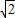 或x=1-
或x=1-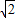 (負值不適合,應舍去),
(負值不適合,應舍去), .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
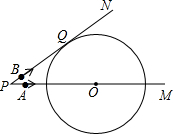 P出發,點A以5cm/s的速度沿射線PM方向運動,點B以4cm/s的速度沿射線PN方向運動.設運動時間為ts.
P出發,點A以5cm/s的速度沿射線PM方向運動,點B以4cm/s的速度沿射線PN方向運動.設運動時間為ts.查看答案和解析>>
科目:初中數學 來源: 題型:
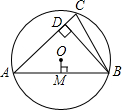 如圖,已知⊙O的半徑為5,銳角△ABC內接于⊙O,弦AB=8,BD⊥AC于點D,OM⊥AB于點M,則sin∠CBD的值等于( )
如圖,已知⊙O的半徑為5,銳角△ABC內接于⊙O,弦AB=8,BD⊥AC于點D,OM⊥AB于點M,則sin∠CBD的值等于( )| A、0.6 | B、0.8 | C、0.5 | D、1.2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•新疆)如圖,已知⊙O的半徑為4,CD是⊙O的直徑,AC為⊙O的弦,B為CD延長線上的一點,∠ABC=30°,且AB=AC.
(2013•新疆)如圖,已知⊙O的半徑為4,CD是⊙O的直徑,AC為⊙O的弦,B為CD延長線上的一點,∠ABC=30°,且AB=AC.查看答案和解析>>
科目:初中數學 來源: 題型:
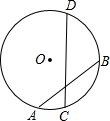 如圖,已知⊙O的半徑為5,兩弦AB、CD相交于AB中點E,且AB=8,CE:ED=4:9,則圓心到弦CD的距離為( )
如圖,已知⊙O的半徑為5,兩弦AB、CD相交于AB中點E,且AB=8,CE:ED=4:9,則圓心到弦CD的距離為( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com