
【題目】正方形ABCD,點E為AB的中點,且BF=![]() BC.
BC.
(1)如圖1,求證:DE⊥EF.
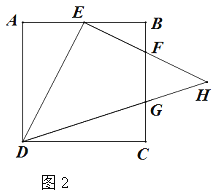
(2)如圖2,若點G在BC上,且CD=3CG,DG、EF交于H點,求![]() 的值.
的值.

【答案】(1)證明見解析;(2)![]()
【解析】
(1)連接DF,設BF=a,利用勾股定理用a表示出DE、EF、DF的長,然后根據勾股定理的逆定理即可得出結論;
(2)連接EG,延長BC至M,使CM=AE,連接DM,可得△DAE≌△DCM,得出DE=DM,∠ADE=∠CDM,推出∠EDM=90°,然后利用勾股定理分別用a表示EG和MG,證出EG=MG,利用SSS可證得△DGE≌△DGM,進而證得∠EDH=45°,利用勾股定理求出DH,即可得出![]() 的值.
的值.
(1)連接DF,設BF=a,則CF=3a,AD=CD=4a,AE=BE=2a,
由勾股定理得:DF=5a,DE= 2![]() a,EF=
a,EF=![]() a,
a,
∴DE2+EF2=( 2![]() a)2+(
a)2+(![]() a)2=25a2,DF2=25a2,
a)2=25a2,DF2=25a2,
∴DE2+EF2=DF2,
∴∠DEF=90,
∴DE⊥EF;
(2)連接EG,延長BC至M,使CM=AE,連接DM,
在△DAE和△DCM中,
 ,
,
∴△DAE≌△DCM(SAS),
∴DE=DM,∠ADE=∠CDM,
∴∠EDM=∠ADC=90°,
∵CD=3CG,
∴CG=![]() a,
a,
∴MG=MC+CG=2a+![]() a=
a=![]() a,
a,
在RtΔBEG中,由勾股定理得:EG=![]() a,
a,
∴EG=MG,
∴△DGE≌△DGM(SSS),
∴∠EDG=∠MDG=45°,
∴△EDH是等腰直角三角形,
∴DH=![]() DE=
DE=![]() EH,
EH,
∴![]() =
=![]() .
.


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在等腰Rt△ABC中,∠BAC=90°,D是AC的中點,CE⊥BD于點E,交BA的延長線于點F.若BF=12,則△FBC的面積為( )

A. 40 B. 46 C. 48 D. 50
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某出租車從停車場出發,沿著東西向的大街行駛,到晚上6時,一天的行駛記錄如下:(向東行駛記為正,向西行駛記為負,單位:千米)-4、+7、-9、+8、+6、-4、-3、+12
(1)到晚上6時,出租車在什么位置?
(2)若汽車每千米耗油0.2升,則從停車場出發到晚上6時,出租車共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在扇形BAD中,點C在 ![]() 上,且∠BDC=30°,AB=2
上,且∠BDC=30°,AB=2 ![]() ,∠BAD=105°,過點C作CE⊥AD,則圖中陰影部分的面積為( )
,∠BAD=105°,過點C作CE⊥AD,則圖中陰影部分的面積為( ) 
A.π﹣2
B.π﹣1
C.2π﹣2
D.2π+1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,對角線AC,BD交于點O,已知∠AOD=120°,AC=16,則圖中長度為8的線段有( )

A. 2條 B. 4條 C. 5條 D. 6條
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,數軸上 A、B 兩點所對應的數分別是 a 和 b,且(a+5)2+|b﹣7|=0.
(1)求 a,b;A、B 兩點之間的距離.
(2)有一動點 P 從點 A 出發第一次向左運動 1 個單位長度,然后在新的位置第二次運動,向右運動 2個單位長度,在此位置第三次運動,向左運動 3個單位長度…按照如此規律不斷地左右運動,當運動到 2019次時,求點P所對應的數.
(3)在(2)的條件下,點 P在某次運動時恰好到達某一個位置,使點 P到點B的距離是點 P 到點 A 的距離的3倍?請直接寫出此時點 P所對應的數,并分別寫出是第幾次運動.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展校園足球運動,某縣城區四校決定聯合購買一批足球運動裝備,市場調查發現:甲、乙兩商場以同樣的價格出售同種品牌的足球隊服和足球,已知每套隊服比每個足球多50元,兩套隊服與三個足球的費用相等,經洽談,甲商場優惠方案是:每購買十套隊服,送一個足球;乙商場優惠方案是:若購買隊服超過80套,則購買足球打八折.
(1)求每套隊服和每個足球的價格是多少?
(2)若城區四校聯合購買100套隊服和a個足球,請用含a的式子分別表示出到甲商場和乙商場購買裝備所花的費用;
(3)假如你是本次購買任務的負責人,你認為到哪家商場購買比較合算?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com