
【題目】如圖,平面直角坐標系中,四邊形OABC是長方形,O為原點,點A在x軸上,點C在y軸上且A(10,0),C(0,6),點D在AB邊上,將△CBD沿CD翻折,點B恰好落在OA邊上點E處.

(1)求點E的坐標;
(2)求折痕CD所在直線的函數表達式;
(3)請你延長直線CD交x軸于點F. ①求△COF的面積;
②在x軸上是否存在點P,使S△OCP=![]() S△COF?若存在,求出點P的坐標;若不存在,請說明理由.
S△COF?若存在,求出點P的坐標;若不存在,請說明理由.
【答案】(1)E(8,0);
(2)y=﹣![]() x+6
x+6
(3)①54;②點P的坐標為(6,0)或(﹣6,0).
【解析】(1)根據折疊的性質知CE=CB=10.在在直角△COE中,由勾股定理求得OE=8;
(2)根據OC=6知C(0,6),由折疊的性質與勾股定理,求得D(10,![]() ),利用待定系數法求CD所在直線的解析式;
),利用待定系數法求CD所在直線的解析式;
(3)①根據F(18,0),即可求得△COF的面積;②設P(x,0),依S△OCP=![]() S△CDE得
S△CDE得![]() ×OP×OC=
×OP×OC=![]() ×54,即
×54,即![]() ×|x|×6=18,求得x的值,即可得出點P的坐標.
×|x|×6=18,求得x的值,即可得出點P的坐標.
(1)如圖,

∵四邊形ABCD是長方形,
∴BC=OA=10,∠COA=90°,
由折疊的性質知,CE=CB=10,
∵OC=6,
∴在直角△COE中,由勾股定理得OE=![]() =8,
=8,
∴E(8,0);
(2)設CD所在直線的解析式為y=kx+b(k≠0),
∵C(0,6),
∴b=6,
設BD=DE=x,
∴AD=6-x,AE=OA-OE=2,
由勾股定理得AD2+AE2=DE2
即(6-x)2+22=x2,
解得x=![]() ,
,
∴AD=6-![]() =
=![]() ,
,
∴D(10,![]() ),
),
代入y=kx+6 得,k=-![]() ,
,
故CD所在直線的解析式為:y=-![]() x+6;
x+6;
(3)①在y=-![]() x+6中,令y=0,則x=18,
x+6中,令y=0,則x=18,
∴F(18,0),
∴△COF的面積=![]() ×OF×OC=
×OF×OC=![]() ×18×6=54;
×18×6=54;
②在x軸上存在點P,使得S△OCP=![]() S△COF,
S△COF,
設P(x,0),依題意得
![]() ×OP×OC=
×OP×OC=![]() ×54,即
×54,即![]() ×|x|×6=18,
×|x|×6=18,
解得x=±6,
∴在x軸上存在點P,使得S△OCP=![]() S△COF,點P的坐標為(6,0)或(-6,0).
S△COF,點P的坐標為(6,0)或(-6,0).


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
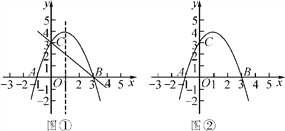
【題目】拋物線y=-x2+2x+3與x軸交于點A、B(點A在點B的左側),與y軸交于點C.
(1)求直線BC的表達式;
(2)拋物線的對稱軸上存在點P,使∠APB=∠ABC,利用圖①求點P的坐標;
(3)點Q在y軸右側的拋物線上,利用圖②比較∠OCQ與∠OCA的大小,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊△ABC和等邊△ECD的邊長相等,BC與CD兩邊在同一直線上,請根據如下要求,使用無刻度的直尺,通過連線的方式畫圖.
(1)在圖1中畫一個直角三角形; (2)在圖2中畫出∠ACE的平分線.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點B在線段AC上,點E在線段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分別是AE,CD的中點。試探索BM和BN的關系,并證明你的結論。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△DBC 中,DB=DC,A 為△DBC 外一點,且∠BAC=∠BDC,DE AC 于 E,

(1)求證:AD 平分△ABC 的外角;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,AC=2AB,點D是AC的中點.將一塊銳角為45°的直角三角板如圖放置,使三角板斜邊的兩個端點分別與A、D重合,連接BE、EC.
 試猜想線段BE和EC的數量及位置關系,并證明你的猜想.
試猜想線段BE和EC的數量及位置關系,并證明你的猜想.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了解學生的課外閱讀情況,隨機抽取了50名學生,并統計他們平均每天的課外閱讀時間t(單位:min),然后利用所得數據繪制成如下不完整的統計表.
課外閱讀時間t | 頻數 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合計 | 50 | 100% |
請根據圖表中提供的信息回答下列問題:
(1)a= ,b= ;
(2)將頻數分布直方圖補充完整;
(3)若全校有900名學生,估計該校有多少學生平均每天的課外閱讀時間不少于50min?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】體育課上,某中學對七年級男生進行跳繩測試,以130個/分鐘為準,超過的次數記為正數,不足的次數記為負數.其中8名男生的成績分別為![]() ,0.
,0.
(1)這8名男生達到標準的百分率是多少?
(2)他們共跳了多少個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com