
【題目】已知:![]() 是最小的正整數,且
是最小的正整數,且![]() 、
、![]() 滿足
滿足![]() ,請回答問題:
,請回答問題:
(1)請直接寫出![]() 、
、![]() 、
、![]() 的值;
的值;
(2)![]() 、
、![]() 、
、![]() 所對應的點分別為
所對應的點分別為![]() 、
、![]() 、
、![]() ,點
,點![]() 為易動點,其對應的數為
為易動點,其對應的數為![]() ,點
,點![]() 在
在![]() 到
到![]() 之間運動時(即
之間運動時(即 ![]() 時),請化簡式子:
時),請化簡式子:![]() (請寫出化簡過程);
(請寫出化簡過程);
![]()
(3)在(1)(2)的條件下,點![]() 、
、![]() 、
、![]() 開始在數軸上運動,點
開始在數軸上運動,點![]() 以每秒
以每秒![]() 個單位長度的速度向左運動;同時,點
個單位長度的速度向左運動;同時,點![]() 和點
和點![]() 分別以每秒
分別以每秒![]() 個單位長度和
個單位長度和![]() 個單位長度的速度向右運動,假設
個單位長度的速度向右運動,假設![]() 秒鐘過后,若點
秒鐘過后,若點![]() 和點
和點![]() 之間的距離表示為
之間的距離表示為![]() ,點
,點![]() 和點
和點![]() 之間的距離表示為
之間的距離表示為![]() .請問:
.請問:![]() 的值是否隨著時間
的值是否隨著時間![]() 的變化而改變?若變化,請說明理由;若不變,請求其值.
的變化而改變?若變化,請說明理由;若不變,請求其值.
【答案】(1) a=1,b=1,c=5;(2) 4x+10,(3)![]() 的值是不會隨著時間
的值是不會隨著時間![]() 的變化而改變,其值為2.
的變化而改變,其值為2.
【解析】
(1)根據b是最小的正整數,即可確定b的值,然后根據非負數的性質,幾個非負數的和是0,則每個數是0,即可求得a,b,c的值;
(2)根據x的范圍,確定x+1,x-1,x+5的符號,然后根據絕對值的意義即可化簡;
(3)根據A,B,C的運動情況即可確定AB,BC的變化情況,即可確定AB-BC的值.
(1)∵b是最小的正整數,
∴b=1.
根據題意得:![]()
∴a=1,b=1,c=5;
(2)當![]() 時,
時,![]()
∴|x+1||x1|+2|x+5|=x+1(1x)+2(x+5)=x+11 x +2x+10=4x+10,
(3)不變.
根據題意可得:運動后點A:![]()
![]()
![]()
![]()
![]()
![]() 的值是不會隨著時間
的值是不會隨著時間![]() 的變化而改變,其值為2.
的變化而改變,其值為2.


科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,BC為⊙O的切線,D為⊙O上的一點,CD=CB,延長CD交BA的延長線于點E. 
(1)求證:CD為⊙O的切線;
(2)若BD的弦心距OF=1,∠ABD=30°,求圖中陰影部分的面積.(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前我市“校園手機”現象越來越受到社會關注,針對這種現象,隨機抽查了某中學九年級的同學,關于手機在中學生中的主要用途做了調查,對調查數據進行統計整理、制作了如下的兩種統計圖,請根據圖形回答問題: 
(1)這次被調查的學生共有人,其中主要用于“上網聊天”的學生人數占抽樣人數的百分比為;
(2)請你將條形統計圖(2)補充完整;
(3)若該校共有3000名學生,請你估計主要使用手機玩游戲的人數大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系上有點A(1,0),點A第一次跳動至點![]() ,第二次點
,第二次點![]() 跳動至點
跳動至點![]() 第三次點
第三次點![]() 跳動至點
跳動至點![]() ,第四次點
,第四次點![]() 跳動至點
跳動至點![]() ……,依此規律跳動下去,則點
……,依此規律跳動下去,則點![]() 與點
與點![]() 之間的距離是( )
之間的距離是( )

A. 2017B. 2018C. 2019D. 2020
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=CB,∠ABC=90°,F為AB延長線上一點,點E在BC上,且AE=CF.

(1)求證:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 于點
于點![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的度數.
的度數.
解:![]() (已知)
(已知)
![]() ___________(同位角相等,兩直線平行)
___________(同位角相等,兩直線平行)
![]() ______(兩直線平行,內錯角相等)
______(兩直線平行,內錯角相等)
又![]() (已知)
(已知)
![]() ___________(等量代換)
___________(等量代換)
![]() ________________
________________
![]() ________________
________________
![]() (已知)
(已知)
![]() ______________(垂直的定義)
______________(垂直的定義)
![]() (等量代換)
(等量代換)
![]() (已知)
(已知)
![]() _____
_____![]() _____
_____![]() (等式的性質)
(等式的性質)
查看答案和解析>>
科目:初中數學 來源: 題型:
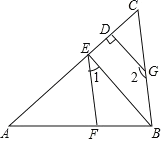
【題目】如圖,已知△ABC中,AB=AC,D為△ABC所在平面內的一點,過D作DE∥AB,DF∥AC分別交直線AC,直線AB于點E,F.
(1)如圖1,當點D在線段BC上時,通過觀察分析線段DE、DF、AB之間的數量關系,并說明理由;
(2)如圖2,當點D在直線BC上,其他條件不變時,試猜想線段DE、DF、AB之間的數量關系(請直接寫出等式,不需證明);
(3)如圖3,當點D是△ABC內一點,過D作DE∥AB,DF∥AC分別交直線AC,直線AB和直線BC于E、F和G. 試猜想線段DE、DF、DG與AB之間的數量關系(請直接寫出等式,不需證明).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年初,由于新冠肺炎的影響,我們不能去學校上課,但是我們“停課不停學”.所以學校派王老師開車從學校出發前往太陽鄉修善村給學生送新書,行駛一段時間后,因車子出故障,途中耽擱了一段時間,車子修好后,加速前行,到達修善村后給學生發完新書,然后勻速開車回到學校.其中![]() 表示王老師從學校出發后的時間,
表示王老師從學校出發后的時間,![]() 表示王老師離學校的距離,下面能反映
表示王老師離學校的距離,下面能反映![]() 與
與![]() 的函數關系的大致圖象是( )
的函數關系的大致圖象是( )
A.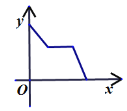 B.
B.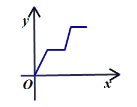
C.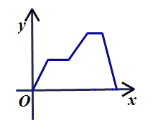 D.
D.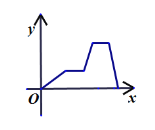
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的文字,解答問題,
例如:∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,∴
<3,∴![]() 的整數部分為2,小數部分為(
的整數部分為2,小數部分為(![]() ﹣2).
﹣2).
請解答:(1)![]() 的整數部分是 ,小數部分是 .
的整數部分是 ,小數部分是 .
(2)已知:5﹣![]() 小數部分是m,6+
小數部分是m,6+![]() 小數部分是n,且(x+1)2=m+n,請求出滿足條件的x的值.
小數部分是n,且(x+1)2=m+n,請求出滿足條件的x的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com