
【題目】已知函數![]() 為二次函數,不等式
為二次函數,不等式![]() 的解集
的解集![]() ,且
,且![]() 在區間
在區間![]() 上的最大值為12.
上的最大值為12.
(1)求函數![]() 的解析式;
的解析式;
(2)設函數![]() 在
在![]() 上的最小值為
上的最小值為![]() ,求
,求![]() 的表達式及
的表達式及![]() 的最小值.
的最小值.
【答案】(1)![]()
(2)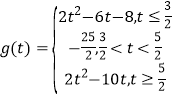
![]() .
.
【解析】
(1)不等式![]() 的解集
的解集![]() ,得出f(x)=m(x﹣5)x,m>0,f(x)在區間[﹣1,3]上的最大值為12.f(﹣1)=12,即可求出解析式.
,得出f(x)=m(x﹣5)x,m>0,f(x)在區間[﹣1,3]上的最大值為12.f(﹣1)=12,即可求出解析式.
(2)根據二次函數的對稱軸和單調性判斷.
(1)∵f(x)是二次函數,不等式f(x)<0的解集為(0,5),
∴f(x)=m(x﹣5)x,m>0,對稱軸x=![]() ,
,
∵f(x)在區間[﹣1,3]上的最大值為12,
∴f(﹣1)=12,
∴m=2,
∴f(x)=2x2﹣10x,
(2)由(1)知,f(x)=2x2﹣10x,
對稱軸是x=![]() ,t≥
,t≥![]() 時,f(x)在[t,t+1]遞增,
時,f(x)在[t,t+1]遞增,
故f(x)min=f(t)=2t2﹣10t,
t<![]() <t+1即
<t+1即![]() <t<
<t<![]() 時,f(x)min=f(
時,f(x)min=f(![]() )=﹣
)=﹣![]() ,
,
t+1≤![]() 即t≤
即t≤![]() 時,f(x)min=f(t+1)=2t2﹣6t﹣8,
時,f(x)min=f(t+1)=2t2﹣6t﹣8,
綜上,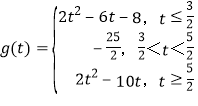 ,
,
則![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx+ ![]() ax2﹣2bx
ax2﹣2bx
(1)設點a=﹣3,b=1,求f(x)的最大值;
(2)當a=0,b=﹣ ![]() 時,方程2mf(x)=x2有唯一實數解,求正數m的取值范圍.
時,方程2mf(x)=x2有唯一實數解,求正數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)與g(x)是定義在同一區間[a,b]上的兩個函數,若函數y=f′(x)﹣g(x)(f′(x)為函數f(x)的導函數)在[a,b]上有且只有兩個不同的零點,則稱f(x)是g(x)在[a,b]上的“關聯函數”.若f(x)= ![]() +4x是g(x)=2x+m在[0,3]上的“關聯函數”,則實數m的取值范圍是( )
+4x是g(x)=2x+m在[0,3]上的“關聯函數”,則實數m的取值范圍是( )
A.![]()
B.[﹣1,0]
C.(﹣∞,﹣2]
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=﹣x3+ax2+bx+c圖象上的點P(1,﹣2)處的切線方程為y=﹣3x+1.
(1)若函數f(x)在x=﹣2時有極值,求f(x)的表達式
(2)若函數f(x)在區間[﹣2,0]上單調遞增,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD與BDEF均為菱形,設AC與BD相交于點O,若∠DAB=∠DBF=60°,且FA=FC.
(1)求證:FC∥平面EAD;
(2)求二面角A-FC-B的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin![]() +
+![]() cos
cos![]() , x∈R.
, x∈R.
(1)求函數f(x)的最小正周期,并求函數f(x)在x∈[﹣2π,2π]上的單調遞增區間;
(2)函數f(x)=sinx(x∈R)的圖象經過怎樣的平移和伸縮變換可以得到函數f(x)的圖象.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩定點F1(﹣1,0),F2(1,0),且![]() 是|PF1|與|PF2|的等差中項,則動點P的軌跡是( )
是|PF1|與|PF2|的等差中項,則動點P的軌跡是( )
A. 橢圓 B. 雙曲線 C. 拋物線 D. 線段
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com