
已知函數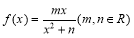 , 在
, 在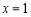 處取得極小值2.
處取得極小值2.
(1)求函數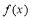 的解析式;
的解析式;
(2)求函數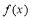 的極值;
的極值;
(3)設函數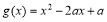 , 若對于任意
, 若對于任意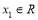 ,總存在
,總存在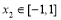 , 使得
, 使得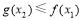 , 求實數
, 求實數 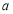 的取值范圍.
的取值范圍.
(1)函數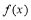 的解析式為
的解析式為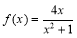 ;(2)
;(2)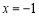 時,函數
時,函數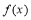 有極小值-2;當
有極小值-2;當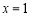 時,函數
時,函數 有極大值2 ;(3)a的取值范圍是(-∞,-1]∪[ 3,+∞).
有極大值2 ;(3)a的取值范圍是(-∞,-1]∪[ 3,+∞).
【解析】
試題分析:(1)根據函數在極值處導函數為0,極小值為2聯立方程組即可求得m,n;(2)由(1)求得函數解析式,對函數求導且讓導函數為0,即可求得極大值和極小值;(3)依題意只需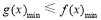 即可,當
即可,當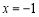 時,函數
時,函數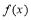 有最小值-2 ,即對任意
有最小值-2 ,即對任意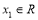 總存在
總存在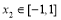 ,使得
,使得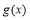 的最小值不大于-2 ;而
的最小值不大于-2 ;而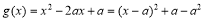 ,分
,分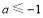 、
、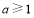 、
、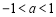 三種情況討論即可.
三種情況討論即可.
試題解析:(1)∵函數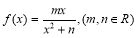 在
在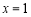 處取得極小值2,∴
處取得極小值2,∴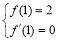 1分
1分
又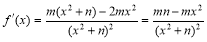 ∴
∴
由②式得m=0或n=1,但m=0顯然不合題意 ∴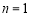 ,代入①式得m=4
,代入①式得m=4
∴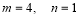 2分
2分
經檢驗,當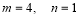 時,函數
時,函數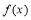 在
在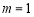 處取得極小值2
處取得極小值2
∴函數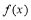 的解析式為
的解析式為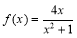 4分
4分
(2)∵函數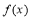 的定義域為
的定義域為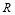 且由(1)有
且由(1)有 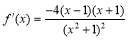
令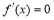 ,解得:
,解得: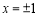
∴當x變化時,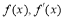 的變化情況如下表:
的變化情況如下表:
x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| — | 0 | + | 0 | — |
| 減 | 極小值-2 | 增 | 極大值2 | 減 |
∴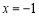 時,函數
時,函數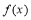 有極小值-2;當
有極小值-2;當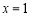 時,函數
時,函數 有極大值2 8分
有極大值2 8分
(3)依題意只需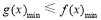 即可.
即可.
∵函數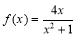 在
在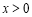 時,
時,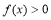 ;在
;在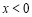 時,
時,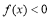 且
且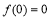
∴ 由(2)知函數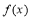 的大致圖象如圖所示:
的大致圖象如圖所示:
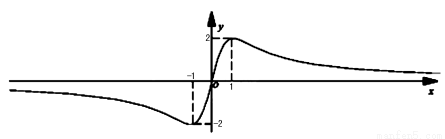
∴當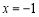 時,函數
時,函數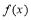 有最小值-2 10分
有最小值-2 10分
又對任意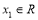 總存在
總存在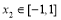 ,使得
,使得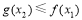 ∴當
∴當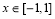 時,
時,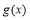 的最小值不大于-2
的最小值不大于-2
又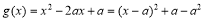
①當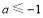 時,
時,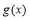 的最小值為
的最小值為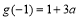 ∴
∴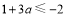 得
得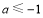 ;
;
②當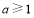 時,
時,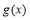 的最小值為
的最小值為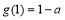 ∴
∴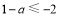 得
得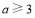 ;
;
③當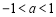 時,
時,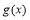 的最小值為
的最小值為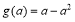 ∴
∴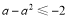 得
得 或
或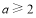
又∵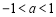 ∴此時a不存在
∴此時a不存在
綜上所述,a的取值范圍是(-∞,-1]∪[3,+∞). 13分
考點:導數的應用、函數思想、分類討論思想.


科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標4.1練習卷(解析版) 題型:填空題
自由落體運動的物體下降距離h和時間t的關系式為h=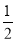 gt2,t=2時的瞬時速度為19.6,則g=________.
gt2,t=2時的瞬時速度為19.6,則g=________.
查看答案和解析>>
科目:高中數學 來源:2015屆湖南張家界市高二上學期期末聯考理科數學試卷(解析版) 題型:填空題
假設關于某設備的使用年限x和所支出的維修費用y(萬元),有如下的統計資料:
x | 2 | 3 | 4 | 5 | 6 |
y | 1.4 | 2.3 | 3.1 | 3.7 | 4.5 |
若由資料可知y對x呈線性相關關系,且線性回歸方程為=a+bx,其中已知b=1.23,請估計使用年限為20年時,維修費用約為________.
查看答案和解析>>
科目:高中數學 來源:2015屆湖南張家界市高二上學期期末聯考理科數學試卷(解析版) 題型:選擇題
從裝有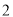 只紅球和
只紅球和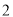 只黒球的口袋內任取
只黒球的口袋內任取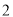 個球,那么互斥而不對立的兩個事件是( )
個球,那么互斥而不對立的兩個事件是( )
A.至少有一個黒球與都是黒球 B.至少有一個黒球與都是紅球
C.至少有一個黒球與至少有 只紅球 D.恰有
只紅球 D.恰有 只黒球與恰有
只黒球與恰有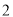 只黒球
只黒球
查看答案和解析>>
科目:高中數學 來源:2015屆湖南張家界市高二上學期期末聯考文科數學試卷(解析版) 題型:填空題
在計算機語言中有一種函數y=int(x)叫做取整函數(也叫高斯函數),它表示不超過x的最大整數,如int(0.9)=0,int(3.14)=3,已知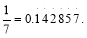 令
令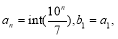 令當n>1時,
令當n>1時,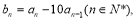 則
則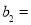 ,
, 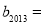 .
.
查看答案和解析>>
科目:高中數學 來源:2015屆湖南張家界市高二上學期期末聯考文科數學試卷(解析版) 題型:選擇題
對具有線性相關關系的變量 ,
,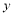 測得一組數據如下表:
測得一組數據如下表:
x | 2 | 4 | 5 | 6 | 8 |
y | 20 | 40 | 60 | 80 | 100 |
根據上表,利用最小二乘法得到它們的回歸直線方程為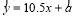 .據此模型預測
.據此模型預測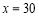 時,
時, 的估計值為( )
的估計值為( )
A. 320 B. 320.5 C. 322.5 D. 321.5
查看答案和解析>>
科目:高中數學 來源:2015屆湖北荊門市高二上學期期末質量檢測理數學試卷(解析版) 題型:填空題
如果隨機變量X~N(-1,σ2),且P(-3≤X≤-1)=0.4,則P(X≥1)=________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com